Using the same polygon the Generalizer (Douglas, tolerance=0) returns different results depending on the orientation of the polygon.
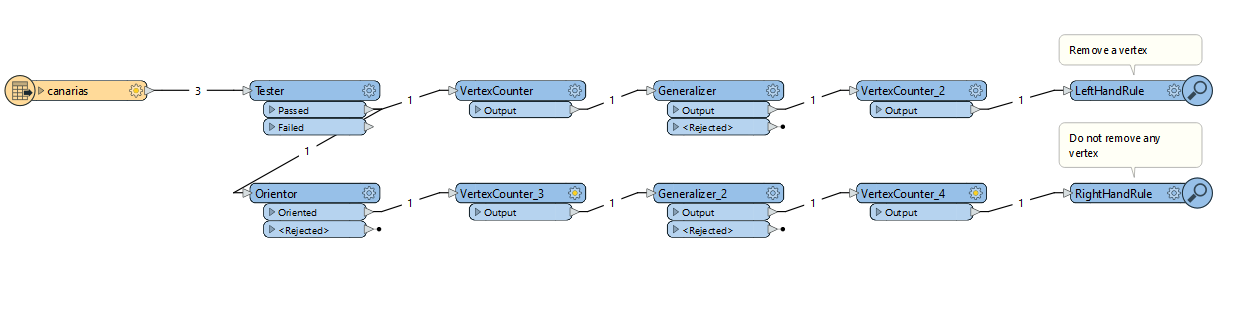
Any explanation?
Using the same polygon the Generalizer (Douglas, tolerance=0) returns different results depending on the orientation of the polygon.

Any explanation?
Best answer by nielsgerrits
If you think something is off with the software, the best thing to do is probably submit a ticket at Safe Software.