Hi @stevenjh, in my observation, the features from your sample data can be classified into these three types.
- Top: non-vertical triangular faces, right-hand-rule
- Bottom: non-vertical triangular faces, left-hand-rule
- Vertical: vertical triangular faces, any rule
In this condition, the faces can be filtered by the sign of z-component value of the normal vector (let's say "vz"). i.e. vz is equal to 0 if the face is vertical, and Top or Bottom can be determined by whether vz is negative or not. In the actual processing, a tolerance should be considered to determine whether a face is vertical, since computational error cannot be avoided always.
From the above consideration, this would be a possible approach.
- Once transform all the faces into 3D triangle polygons.
- Calculate the normal vector based on coordinates of 3 vertices for each triangle.
- Restore the faces (transform the triangles into faces).
- Classify them into Top, Bottom, and Vertical by the z-component value of the normal vector.
- Aggregate them to create surface (IFMEMultiSurface) geometries for each part.
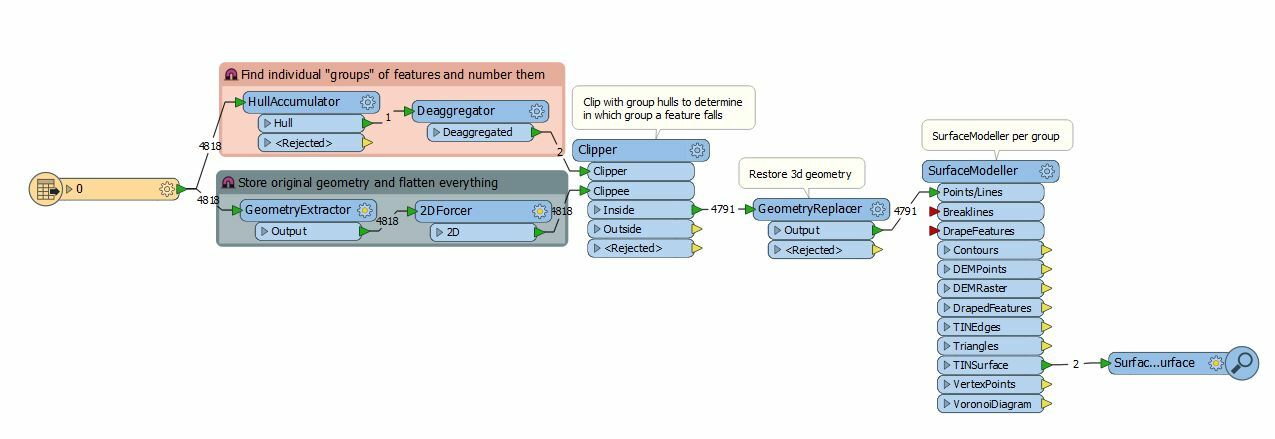
See also the attached example workspace: extract-top-surface-example.fmwt (FME 2015.1.3+)
Note that the approach is only applicable to the same condition as the sample. Different condition requires different approach. First of all, need an inspection about the source data with FME Data Inspector.