Skip to main content
  • EN

I have a set of polygons which has been clipped at one point in time. I would like to dissolve them back together but only along the path originally used to clip them. I don't want to dissolve all polygons touching each other.

My approach so far has been to locate the edges of the polygons I would like to remove and I have marked those in the image below (I have the markings as features). I don't have a common ID on the polygons I would like to dissolve, so I haven't found a way to group the polygons to dissolve them in that way, since one polygon might have more than one marker attached.

How can I achieve what I have outlined below?

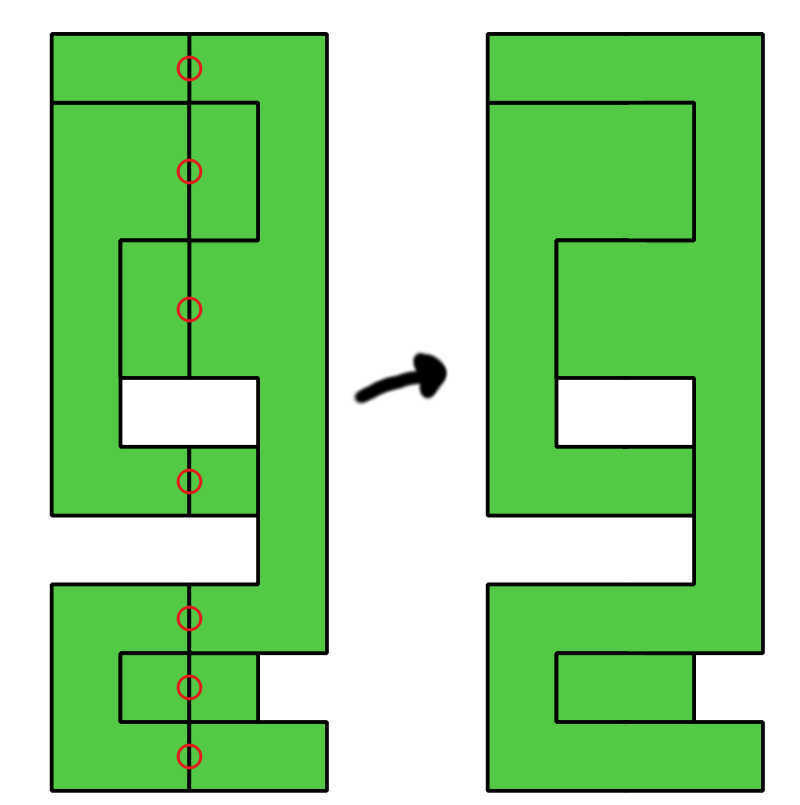
Reference:

If your polygons have a common ID that defines their original composition, you could use that as a Group By in the Dissolver.

If your polygons have a common ID that defines their original composition, you could use that as a Group By in the Dissolver.

I forgot to mention that I don't have a common ID anymore 😞 What you see is what I have.

 

 

I forgot to mention that I don't have a common ID anymore 😞 What you see is what I have.

 

 

Do you have the red circles (I suppose that's what you mean by markings)? If yes, could you post a small sample dataset here?
Do you have the red circles (I suppose that's what you mean by markings)? If yes, could you post a small sample dataset here?
Its attached to the question.

 

 

chau

Create id's for the circles.

Spatial relate with the objects.

Create a string from the list using a listconcatenator. (or query the list)

Compare lists and create a group id.

Use this group id to dissolve.

remove-intersecting-lines.fmw Hi @chau I would use a SpatialFilter to identify the lines to be removed and then rebuild the polygons.

remove-intersecting-lines.fmw Hi @chau I would use a SpatialFilter to identify the lines to be removed and then rebuild the polygons.

Nice solution!

remove-intersecting-lines.fmw Hi @chau I would use a SpatialFilter to identify the lines to be removed and then rebuild the polygons.

Hi Dan, thank you for the very elegant solution - it works really nice!

 

 

Reply


Community Stats

30,196
Posts
114,615
Replies
37,859
Members
Terms & ConditionsCookie settings
A product of
Safe Software respectfully acknowledges that we live, learn and work on the traditional and unceded territories of the Kwantlen, Katzie, and Semiahmoo First Nations.