I want to summarized the polygons (see picture) to bigger polygons.
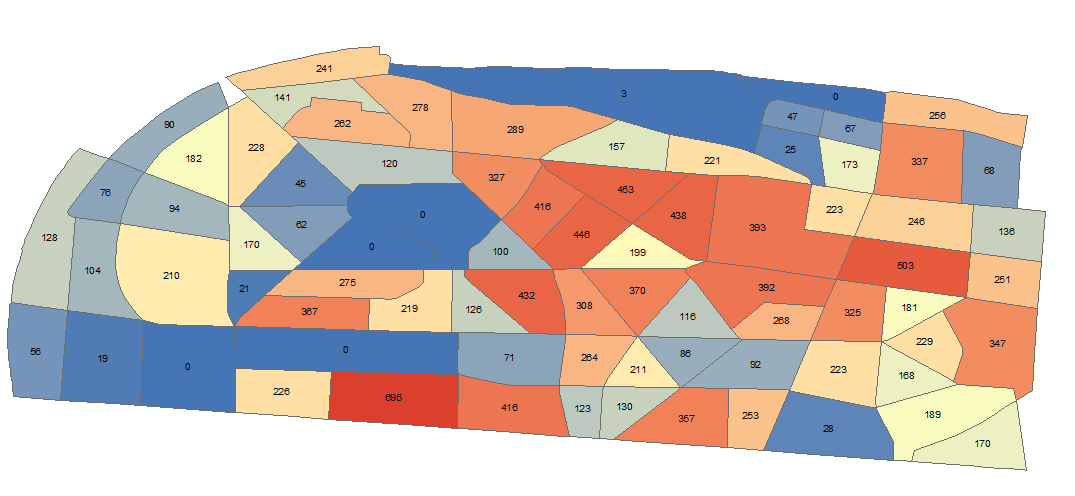
The polygons should be summarized by their number in the middle to around 1000 (+- 100).
At the End there are a lot of polygons with a number around 1000.
Page 1 / 1
This might need more detail as to what particular problem is being solved. The particular question you've posed is an optimisation question without a high degree of constraints, that would instead likely need to be fed to an external Genetic Algorithm engine, and only use FME to output the Topological relationships of the polygon edges to the GA engine that could find which particular groups of properties gives the "best fit" of summing to 1,000.
However, if you are instead trying to assign Eg. Demands onto an underlying network by "grouping up" small, detailed, area loads to "lumpier" area loads, there are other ways of doing this in a constrained way, like using Voronois/Thiessen Polygons around network load points.
If you are trying to group the parcels into 100 groups i.e. 0 - 99, 100 - 199, 200 - 299, etc, why not trying the AttributeRangeMapper transformer http://docs.safe.com/fme/2019.0/html/FME_Desktop_Documentation/FME_Transformers/Transformers/attributerangemapper.htm
This could be made into an infinetly complex question, depending on what is your preferred outcome.
1. Do you want the new polygons to consist of roughly the same number of subpolygons, meaning that you prefer ((500+300+100+100) + (400+200+200+200)) over ((500+300+200) + (400+200+200+100+100)?
2. Does shape matter? Do you want your new polygons to be as condensed as possible, i.e. as close to an ideal hexagon pattern as possible, or would you accept a long sliver of (241+3+0+256+68+136+251)?
3. Would you accept donuts, where (275+367+219+126) is surrounded on all sides by (170+0+100+432+71+0+0+210+21)?
Good luck! :-)
If you are trying to group the parcels into 100 groups i.e. 0 - 99, 100 - 199, 200 - 299, etc, why not trying the AttributeRangeMapper transformer http://docs.safe.com/fme/2019.0/html/FME_Desktop_Documentation/FME_Transformers/Transformers/attributerangemapper.htm
Hi,
this doesnt work for this problem.
This could be made into an infinetly complex question, depending on what is your preferred outcome.
1. Do you want the new polygons to consist of roughly the same number of subpolygons, meaning that you prefer ((500+300+100+100) + (400+200+200+200)) over ((500+300+200) + (400+200+200+100+100)?
2. Does shape matter? Do you want your new polygons to be as condensed as possible, i.e. as close to an ideal hexagon pattern as possible, or would you accept a long sliver of (241+3+0+256+68+136+251)?
3. Would you accept donuts, where (275+367+219+126) is surrounded on all sides by (170+0+100+432+71+0+0+210+21)?
Good luck! :-)
hi,
1. the number of subpolygons is irrelevant. it is possible to have this solution "((500+300+200) + (400+200+200+100+100)"
2. it is not ideal for this problem (long silver) , but when there is ni other way, so i could accept it.
3. Donuts are not an option, because these are electoral districts.
hi,
1. the number of subpolygons is irrelevant. it is possible to have this solution "((500+300+200) + (400+200+200+100+100)"
2. it is not ideal for this problem (long silver) , but when there is ni other way, so i could accept it.
3. Donuts are not an option, because these are electoral districts.
For electoral districts you might want to take polling stations into consideration and use them as condensation nuclei.
For electoral districts you might want to take polling stations into consideration and use them as condensation nuclei.
These are not fixed values, so it doesnt help.
These are not fixed values, so it doesnt help.
Numbers, polygon shapes and points for polling stations can all be different each time the workspace is run. I was just suggesting an extra layer of complexity to the problem. ;-)