Having trouble extending a line to the edge of the polygon it is in.
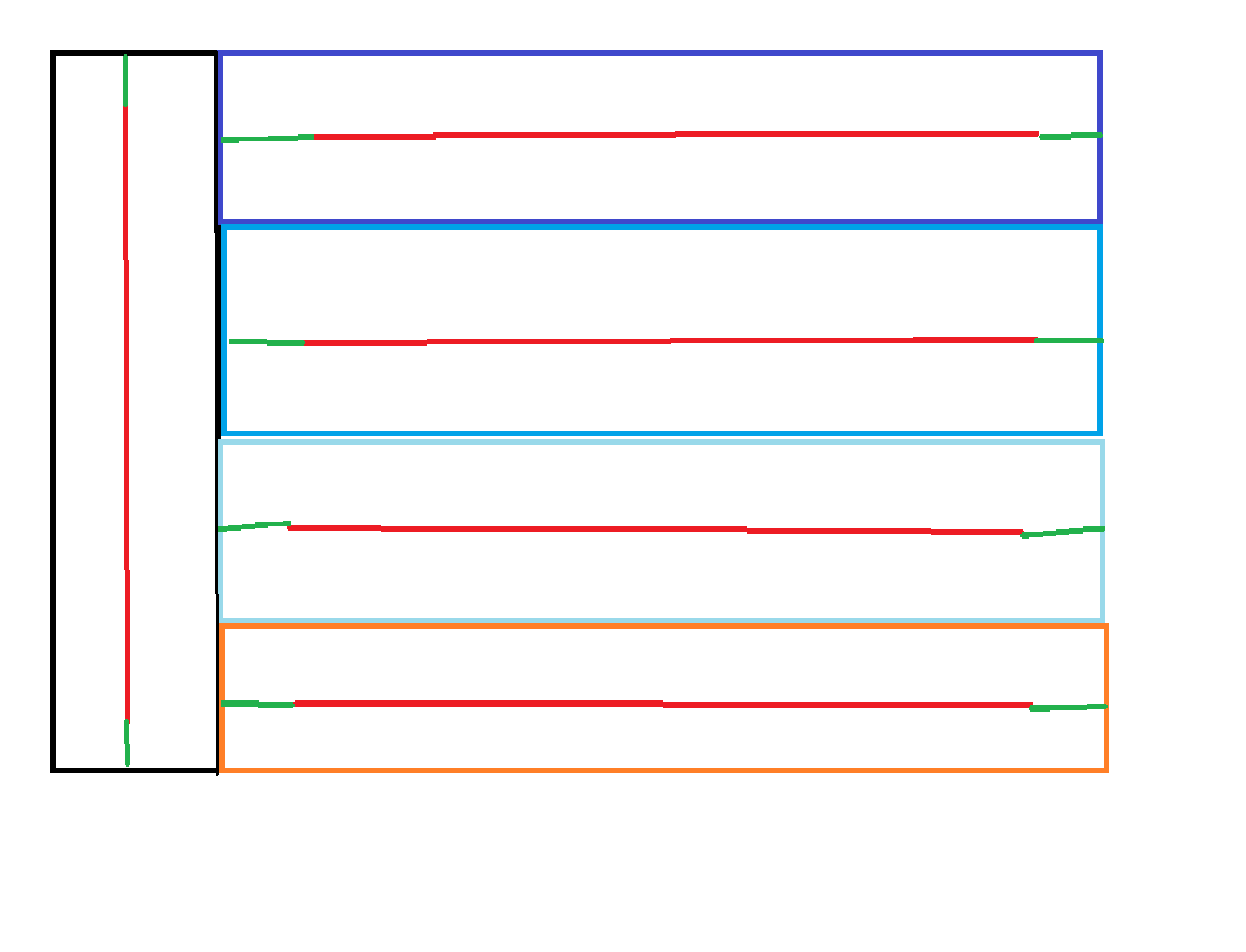 The above example are boxes (different colours) and centre lines (red lines) both as a separate datasets and an attribute that contains the ID connects them if needed. I would like to extend all the lines straight forward (both ways, thus adding the green line) until it touches the edge of the polygon it is in, similar performance as the Extend function in AutoCAD. Is there a similar transformer that does this with two datasets like this?
The above example are boxes (different colours) and centre lines (red lines) both as a separate datasets and an attribute that contains the ID connects them if needed. I would like to extend all the lines straight forward (both ways, thus adding the green line) until it touches the edge of the polygon it is in, similar performance as the Extend function in AutoCAD. Is there a similar transformer that does this with two datasets like this?
I tried the line extender and clipping and also the snapper but without satisfying results.










