I have to transform a series of points to a line consisting of cubic Bezier curves. I couldn't find a function to do that in existing transformers or the Python API of FME Objects. The Generalizer (NURBfit algotirhm) creates a spline curve, but it's not exact cubic Bezier curves. The expected line has to pass through the both ends of each 3 segments.
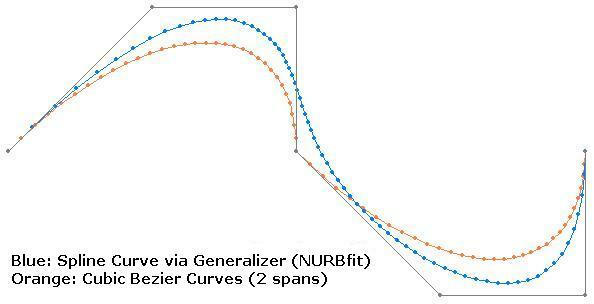
So, I wrote the following script. Is this the "re-invention of the wheel"? If you know an existing function (transformer or Python function) that creates cubic Bezier curves based on control points, please let me know.
-----
import fmeobjects class CubicBezierCurveReplacer(object): def __init__(self): self.set_coefficients(32) def set_coefficients(self, n): self.n = n r = 1.0 / float(self.n) s = range(0, self.n) self.k0 = [(1.0 - (r * m))**3 for m in s] self.k1 = [3.0 * (r * m) * (1.0 - r * m)**2 for m in s] self.k2 = [3.0 * (1.0 - (r * m)) * (r * m)**2 for m in s] self.k3 = [(r * m)**3 for m in s] def bezier_coords(self, p): coords = [] x0, x1, x2, x3 = p[0][0], p[1][0], p[2][0], p[3][0] y0, y1, y2, y3 = p[0][1], p[1][1], p[2][1], p[3][1] for i in range(1, self.n): x = self.k0[i] * x0 + self.k1[i] * x1 + self.k2[i] * x2 + self.k3[i] * x3 y = self.k0[i] * y0 + self.k1[i] * y1 + self.k2[i] * y2 + self.k3[i] * y3 coords.append((x, y)) return coords def input(self, feature): # If the number of coordinates is less than 2, return nothing. if feature.numCoords() < 2: return # Get all coordinates of the input feature as control points. points = feature.getAllCoordinates() # Append coordinates while (number of control points - 1) # is not divisible by 3 evenly. while (len(points) - 1) % 3 != 0: points.append(points[-1]) # Create cubic Bezier curves. bezier = feature.cloneAttributes(); bezier.setGeometryType(fmeobjects.FME_GEOM_LINE) bezier.setCoordSys(feature.getCoordSys()) bezier.addCoordinate(points[0][0], points[0][1]) for i in range(3, len(points), 3): bezier.addCoordinates(self.bezier_coords(points[i - 3 : i + 1])) bezier.addCoordinate(points[i][0], points[i][1]) self.pyoutput(bezier) def close(self): pass -----
Takashi





