Hi, I'm a bit stuck and would need some help.
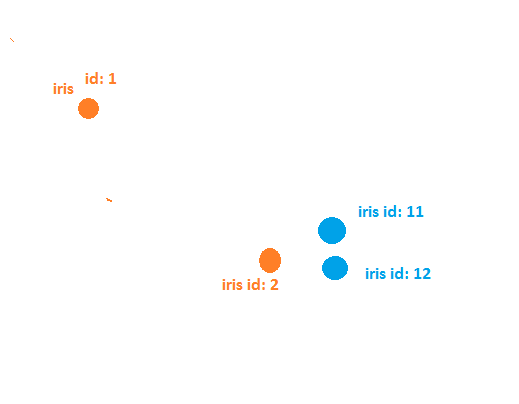
As you can see 2 point layers as shown in the image with different colors. All the points have same name 'iris' though their ids are different.
I need to match the closest same name but the ids shouldnt repeat.
For example: here in the below case iris id 11 and id 12 have iris id 2 as their closest. But what I'm wanting as the output is that if iris id 12 gets closest match as iris id 2 then for iris id 11 it should not consider iris id 1 and check for next point which hasnt got a match with any other point yet i.e. iris id 1.
Let me know if there is any possible solutions for it.
Thank you.