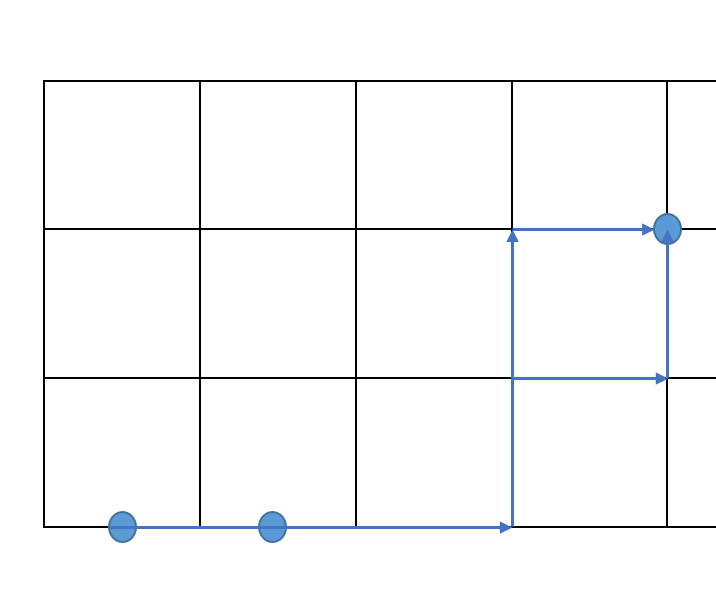
I am currently creating a network by running nodes to a central point, using a 2d Grid as my network.
I am noticing that points that should follow a similar route, sometimes take a slightly different path see below. I'm wondering if there is anything i'm missing to try and avoid this?