Skip to main content
  • EN

Hi! A seemingly simple task for FME fails me, and I need advice. I made this dummy image to explain.

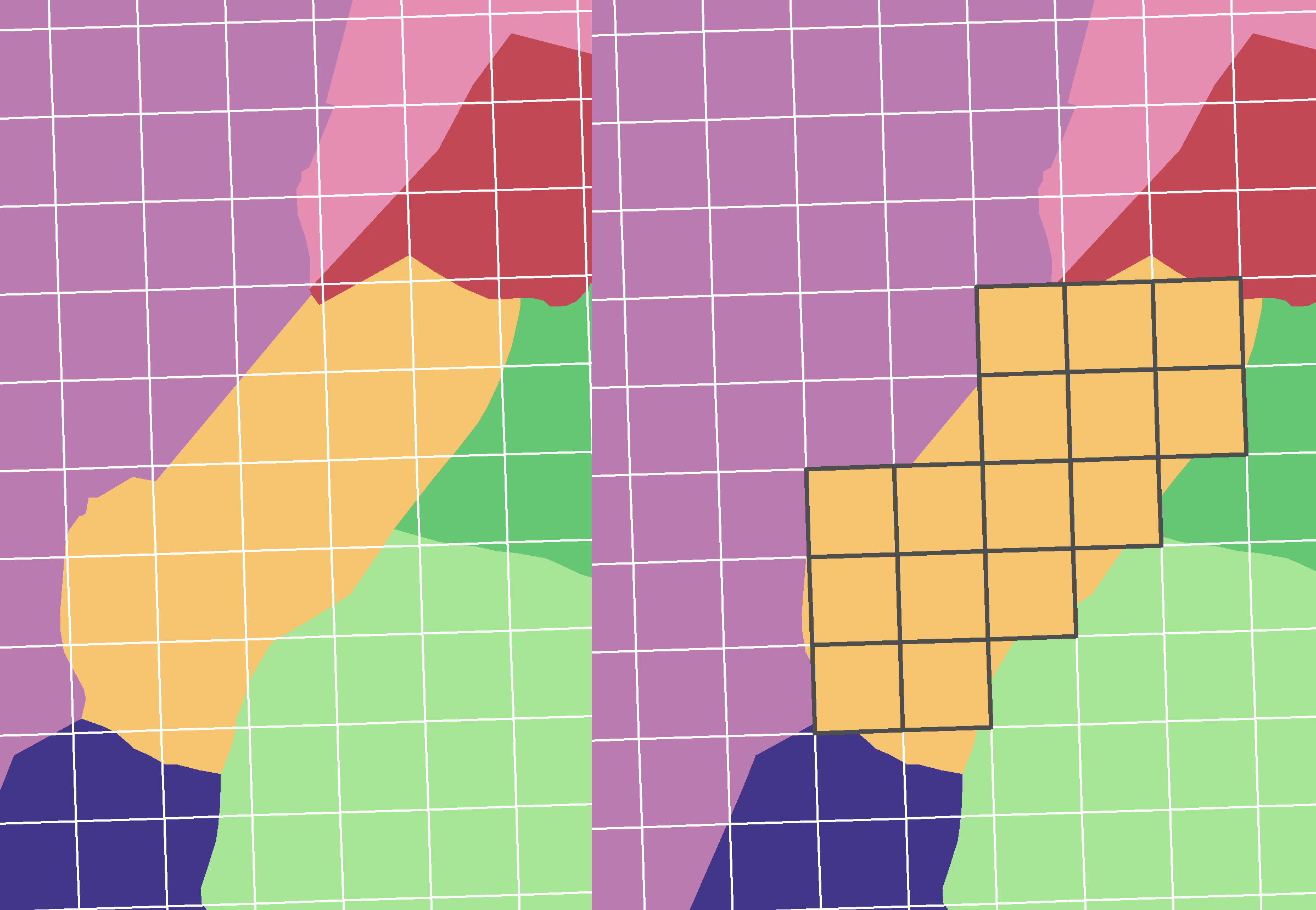
I have a polygon grid (white), and a dataset of polygons (multicolored). The task is to collect some attributes from the polygons, based on the proportion of overlap, so that each grid square gets attributes from the one polygon with the largest overlapping percentage. The image to the right shows the desired output (black bordered squares) for the orange polygon.

I have been through the spatial relator and area on area overlayer to no avail. I am aware of similar questions on this forum, but no good answers. Those offered are very convoluted.

If only the area on area overlayer could tell me the percentage of overlap, and not only the number of overlapping features, I could work from there.

Or is there a transformer that I have yet to find?

Regards, Mats.E

Hi @matself, the area on area overlayer (AOAO) is the right transformer for part of the job, it will split all the polygons.

So if you calculate the initial area (m2) of the polygons and the area (m2) of the polygons resulting form the AOAO, you can calculate the majority of the area (or percentage) and that wat decide which attributes should be used.

I would make use of the list option on the AOAO to capture all involved attributen.

Its a puzzle that needs some thinking and no single transformer will do the job.

Hi @matself, alternatively, this workflow might work for the job.

  1. Save the original square geometry of every grid polygon as an attribute with the GeometryExtractor (Geometry Encoding: FME Binary).
  2. Add a Clipper to the workspace. Send the multi-colored polygons to the Clipper port, send the grid polygons to the Clippee port. Check the 'Merge Attributes' option of the Clipper transformer.
  3. Connect an AreaCalculator to the Inside port of the Clipper to calculate area for every clipped feature.
  4. Sort them by area descending with the Sorter.
  5. Pick first feature for each original grid with the DuplicateFilter (Key Attributes: <unique ID of each grid>). Here, the largest fragment is selected for each grid.
  6. Restore the original square geometry for each selected feature with the GeometryReplacer.

Hi @matself, alternatively, this workflow might work for the job.

  1. Save the original square geometry of every grid polygon as an attribute with the GeometryExtractor (Geometry Encoding: FME Binary).
  2. Add a Clipper to the workspace. Send the multi-colored polygons to the Clipper port, send the grid polygons to the Clippee port. Check the 'Merge Attributes' option of the Clipper transformer.
  3. Connect an AreaCalculator to the Inside port of the Clipper to calculate area for every clipped feature.
  4. Sort them by area descending with the Sorter.
  5. Pick first feature for each original grid with the DuplicateFilter (Key Attributes: <unique ID of each grid>). Here, the largest fragment is selected for each grid.
  6. Restore the original square geometry for each selected feature with the GeometryReplacer.
I think this is about the best method. You could replace pts 4 and 5 with a single StatisticsCalculator - group by grid ID, analyze area, record the max value, and use the Summary output port - but that's just a variation. The general method is the same.

 

 

Basically split the polygons and then calculate area, because I can't think of a single FME transformer that will split a polygon and divide numeric attributes proportionately.

 

Hi!

Thanks for suggestions. They are more or less the same as those already on this list.

Apparently, this is the best FME can do. I am rarely disappointed with FME, but this seems a very straightforward spatial process which ought to be built-in. And not a puzzle that needs some thinking.

Regards, Mats.E

Hi!

Thanks for suggestions. They are more or less the same as those already on this list.

Apparently, this is the best FME can do. I am rarely disappointed with FME, but this seems a very straightforward spatial process which ought to be built-in. And not a puzzle that needs some thinking.

Regards, Mats.E

Hi, Well you can suggest it for implementation...

 

 

Reply


Community Stats

30,123
Posts
114,333
Replies
37,751
Members
Terms & ConditionsCookie settings
A product of
Safe Software respectfully acknowledges that we live, learn and work on the traditional and unceded territories of the Kwantlen, Katzie, and Semiahmoo First Nations.