Skip to main content
  • EN
Question

FME Challenge: Count the maximum number of non overlapping circles!

  • 12 February 2013
  • 3 replies
  • 29 views
Hi all,

 

 

I've a very interesting FME challenge. Any ideas and suggestions how to solve this are very welcome.

 

 

I've some parcels with irregular shapes and I want to know the maximum of circles (with a radius of 2,5 meter, diameter is 5m)) can be placed inside these parcels without overlap of the circles and without crossing the parcel boundaries.

 

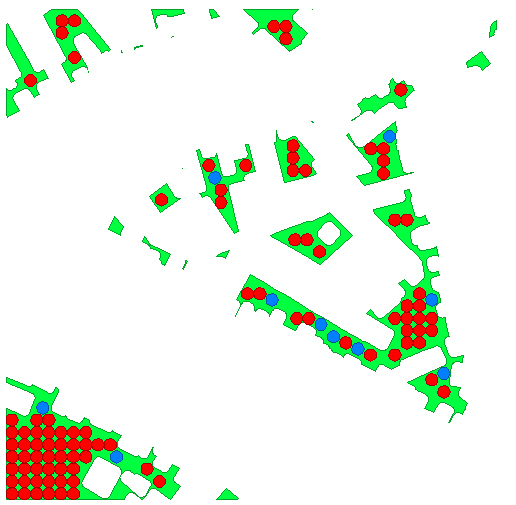
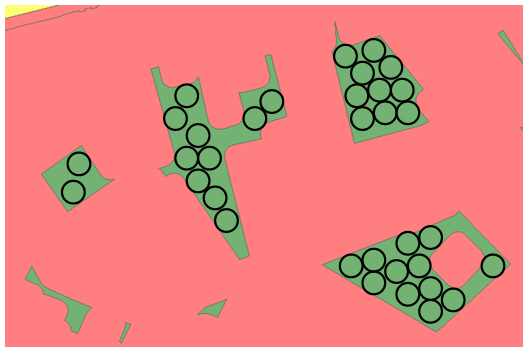
Below you can see what I mean:

 

 

The green polygones are the irregular shaped parcels. I would like to know the maximum number of black cirkels that fit in each of the parcels.

 

 

 

Some remarks:

 

- The solution I'm looking for doesn't have to be exact, but should be a good estimation.

 

- The solution doesn't need to give me the circles (but it would be nice), but just the number of circles is fine as well

 

 

I have already some ideas, but some good extra suggestions are welcome.

 

- My first idea would be something like this:

 

1) create regular grid with circles with radius of 2.5 m, but spaced 1 by 1 m (so overlapping)

 

2) select all circles which are completely within the green parcel

 

3) for each parcel, select the circle which is the closest to the boundary

 

4) for each parcel, deselect the circles which intersect with the circle of step 3

 

5) for each parcel, select the circle which is the second closest to the boundary

 

6) for each parcel, deselect the circles which intersects with the circle of step 5

 

and so on...

 

 

Thanks in advance

 

 

Bruno

3 replies

sigtill
Rank
Userlevel 1
Badge +24
Instead of the grid for the whole area I would create a grid from the bounding box of each feature. Based on this estimate the maximum number of circles that can be inside, and also estimate a most likely number of circles. Then som iterations would be necessary perhaps with some Artificial Intelligence algorithm.
The real SigTill
K
Badge +5
Interesting question, would be fun to see the result if you have implemented some solution in FME.  I don't think you're going to find an optimal answer, but a reasonable estimate should be possible. If you are going for a repeated grid center solution, keep in mind that the most efficient way of packing circles is in a hexagonal layout.

 

 

The simplest approach would be to create a filled space of hexagonally distributed circles, covering the bounding box as Sig suggested, and counting the circles that are completely covered by the parcel. You could add some form of local search in the form of Hillclimbing, Simulated annealing or Random search, but in my opinion a small number of iterations which move the grid in predetermined directions will give you a good estimate.

 

 

A different approach would make the assumption that the best packing has circles touching the edge of the parcel. If you do a negative Buffer with -circleradius on the parcels, you can start by fitting as many circles as possible (perhaps trying different starting positions) on the buffered boundary. You can count these circles, clip the parcelpolygon with them, and repeat the abovementioned steps.

 

 

If you have time, try a few methods and make it a competition, I'm curious to see how the different methods would perform.
B
Hello,

 

 

Thanks for the reactions.

 

This is the solution of something I just implemented:

 

 

 

 

Because I'm affraid of using iterations (would be nefast for performancy, my area is a lot bigger than just this sample), I used a 'simpler' approach which works well enough.

 

 

If someone is interested in what I did; here are the steps:

 

 

1. Create unique ID for each parcel

 

2. Create Bounding Box for each Parcel

 

3. Create grid (2.5 by 2.5 meters) of points in bounding box in each parcel and keep attributes _column and _row (they will be important later on)

 

4. Throw away the points falling outside the parcel (for performancy I first do this step before I do an overlay with the circles, step 6)

 

5. Buffer the points with radius 2.5 m (remark: they overlap eachother)

 

 

6. Throw away the circles which are not completely within the parcel

 

Now there is a group of circles falling completely within the parcel. But there is still overlap.

 

7. For each parcel, look for the most south-western circle which is kept and log its _column en _row attribute.

 

8. if the column-attribute is even, throw away all circles with odd colum-attribute, if the column attribute is odd, throw away all circles with even column attribute.

 

9. repeat the same for row-attribute. (so only keep even or odd rows)

 

(step 8 and 9) will nicely removed all the even of odd lines/rows, depending on the lower left circle.

 

 

Now I have the red circles of the drawing. (with a specific pattern as you see, without overlap, based on the eveness/oddness of the most lower left circle.)

 

 

10. One extra iteration is add. Check if there is still som parcel area which can be covered by circles which were removed in step (8) or (9).

 

If yes, repair them and uses the same method as in step 8 and 9 to prevent overlap.

 

 

So, it is not the best theoretical solution (you can't do that without iterations and dependencies), but this solution is sufficient for the purpose I'm using it.

 

Reply


Community Stats

29,635
Posts
112,623
Replies
37,285
Members
Terms & ConditionsCookie settings