hello
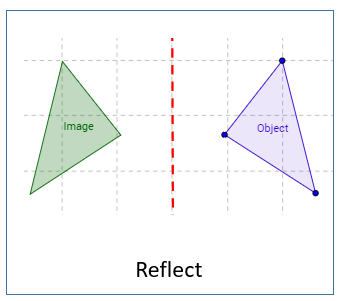
How should I proceed to build the opposite (image) of a polygone (object) with respect to a line?
hello
How should I proceed to build the opposite (image) of a polygone (object) with respect to a line?

Best answer by arthy
Thanks @jdh, @gio, @pratsch
Based on your comments/answers, this is What I did to obtained an "approximate solution":
This is an illustration where the part of the feature contained in a specific small right rectangle was reflected in the corresponding small left rectangle.
