Skip to main content
  • EN

We recently moved some processes from Esri tools into FME. One of these has a slope calculation component. We expected to see minor differences between Esri/FME but instead we are seeing differences of up to 15 degrees difference.

Further investigation showed that by default, Esri uses a planar based algorithm. FME (and QGIS) only use a geodesic based algorithm. Esri does also have the option of using geodesic.

The original Esri process was using the default planar algorithm. When these are compared to the geodesic outputs (FME, Esri and QGIS) considerable differences are apparent. Comparing the three different geodesic outputs shows that the results are (almost) the same – as expected.

This difference has considerable ramifications for the application using these slope values. Looking at Esri documentation, it does state the geodesic is ‘more accurate’, but this doesn’t explain the 15 degree differences we’re seeing.

We have raised this question with Esri, but are wondering if anyone here has an explanation as to why such a difference is apparent?

 

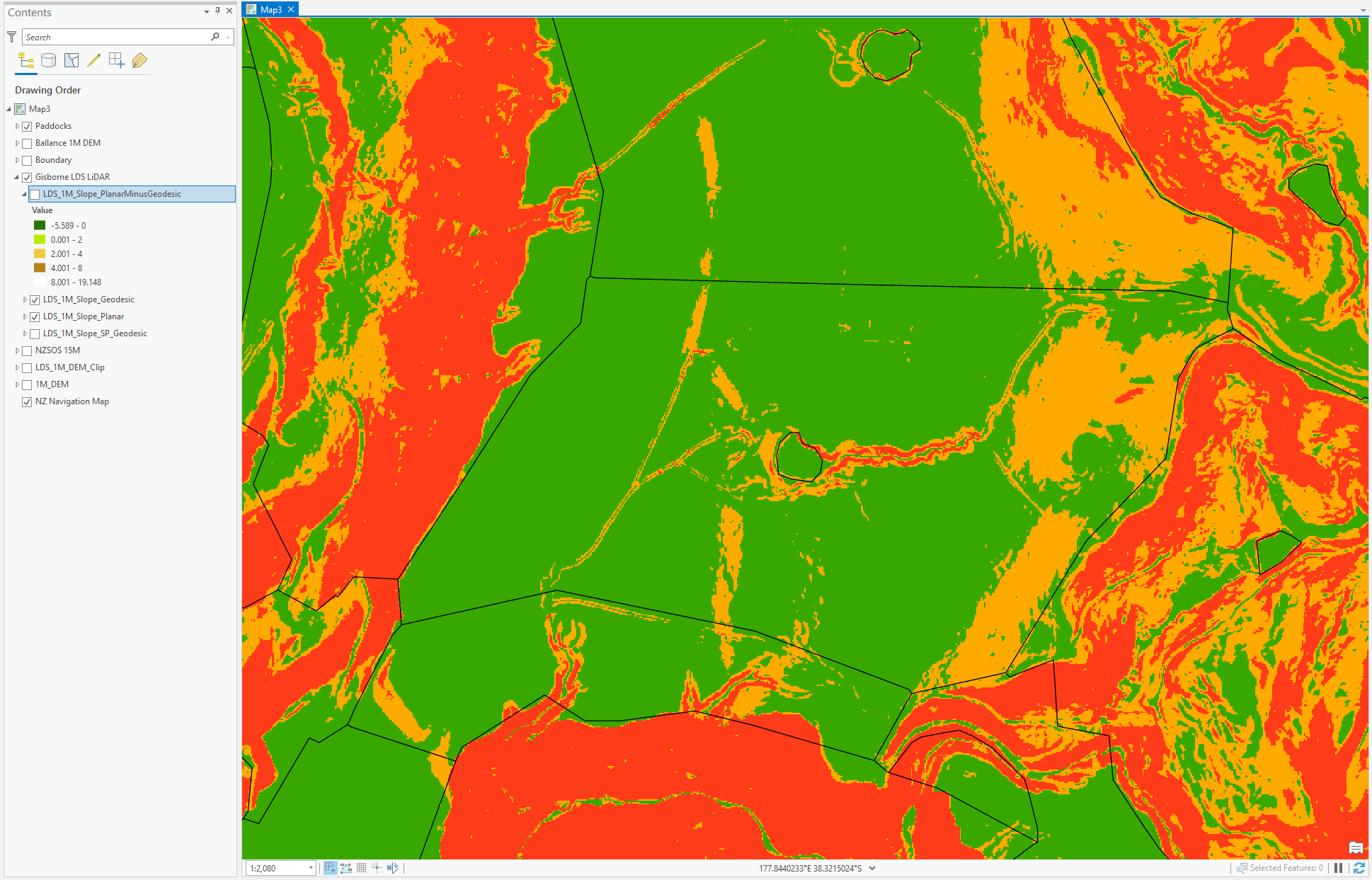
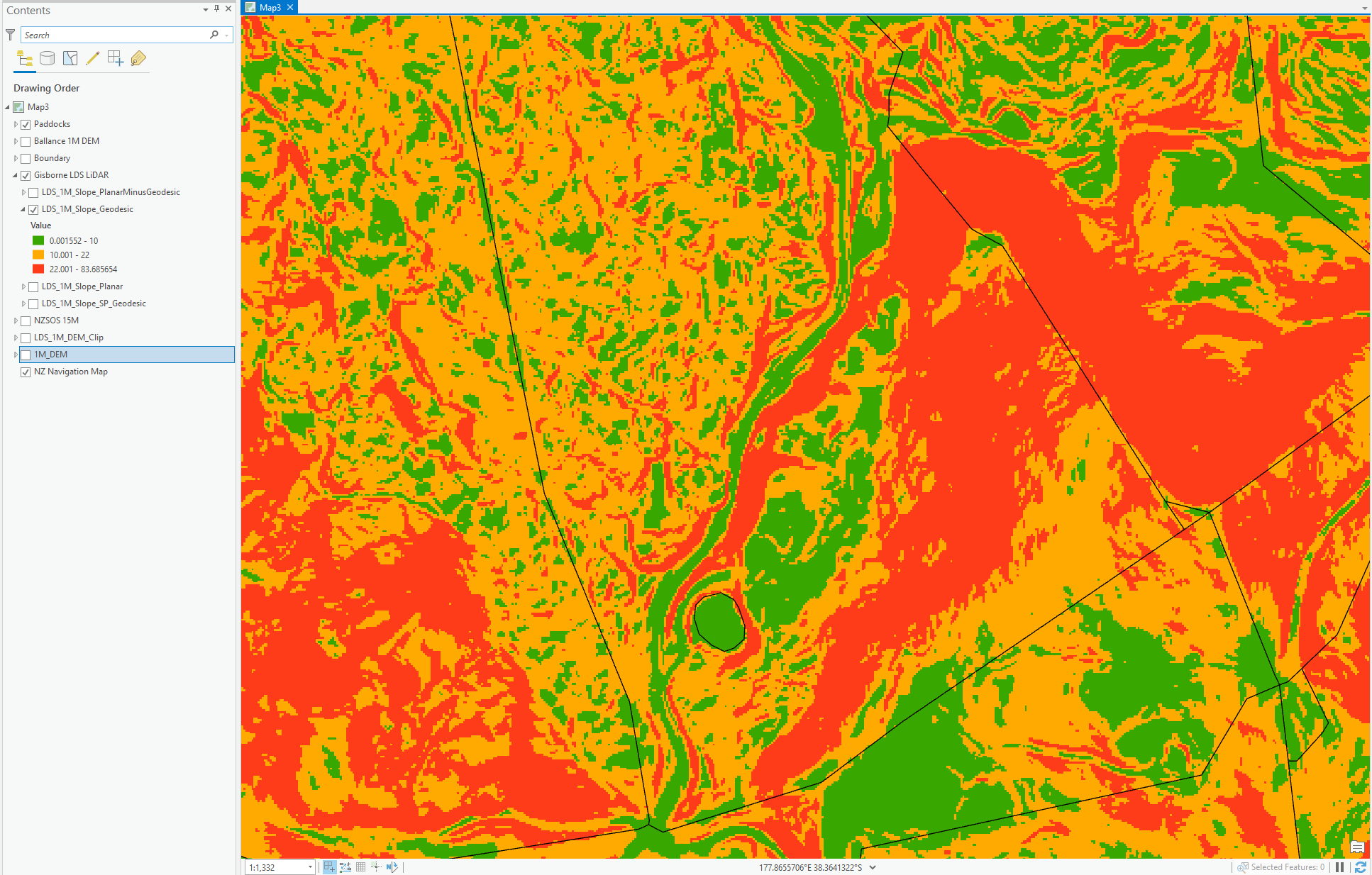
Here are some examples, the slope maps are Green (0-10), Orange (10-22) and Red (22+)

Planar:Planar_2Planar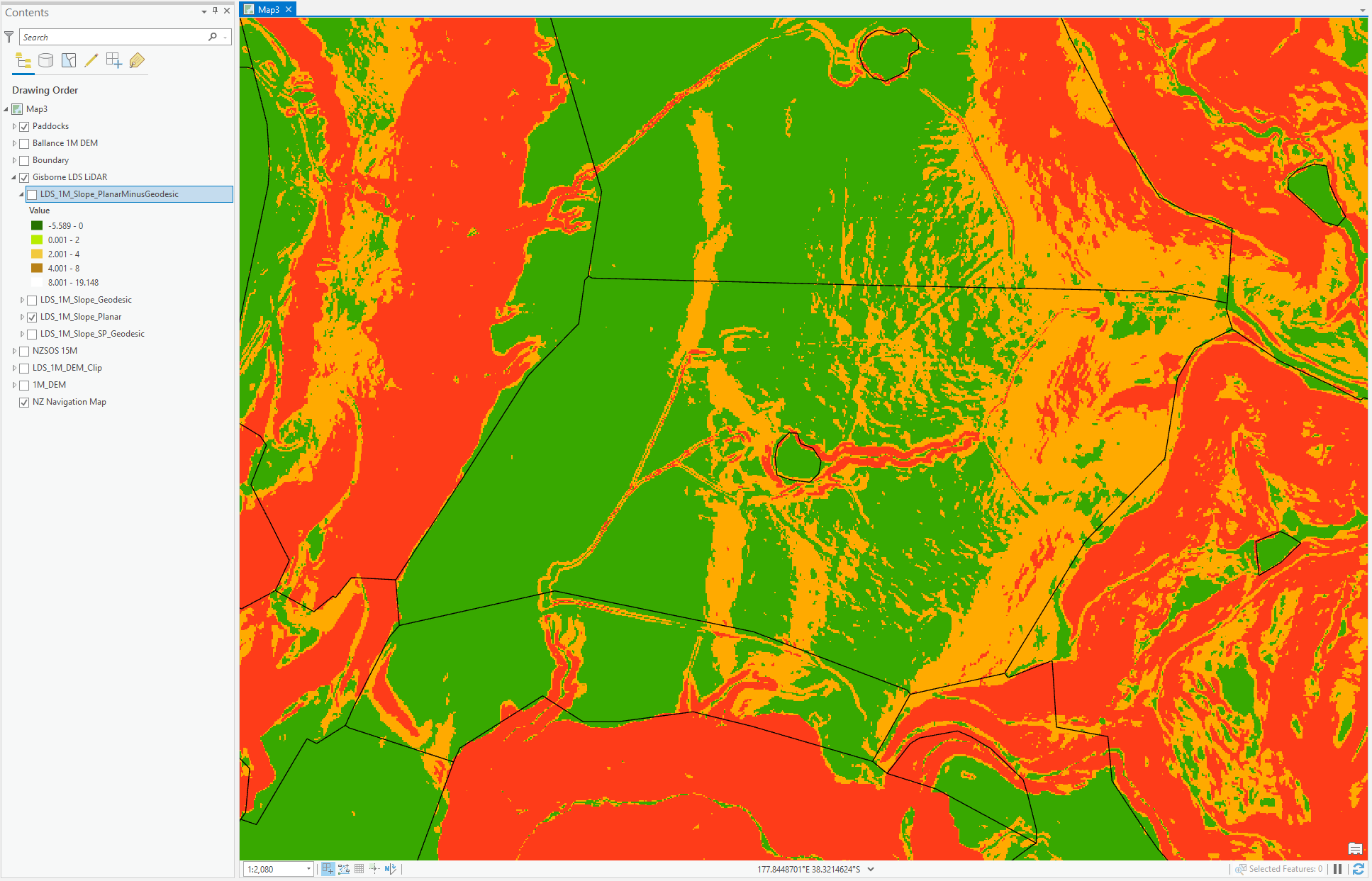Geodesic:

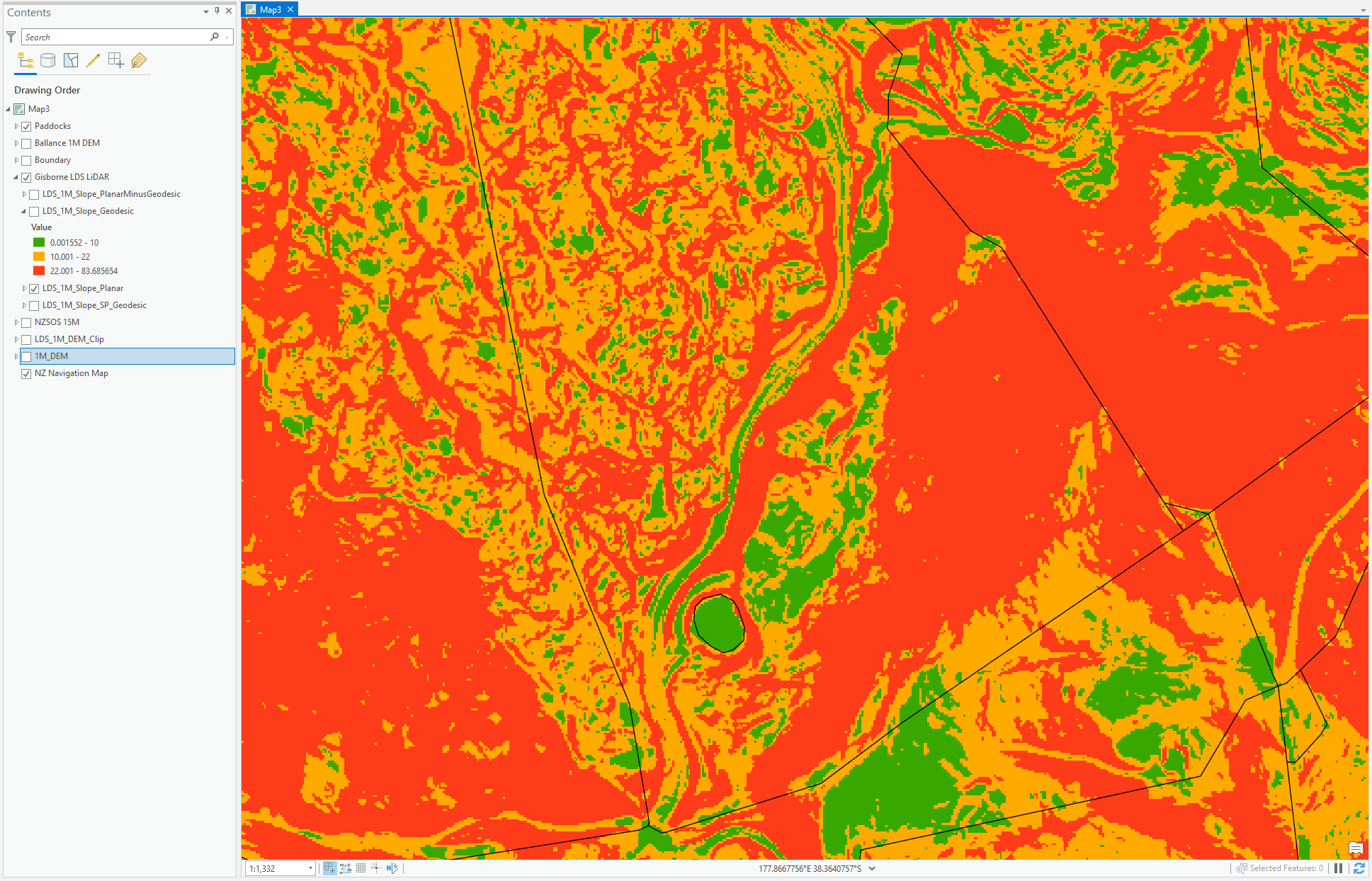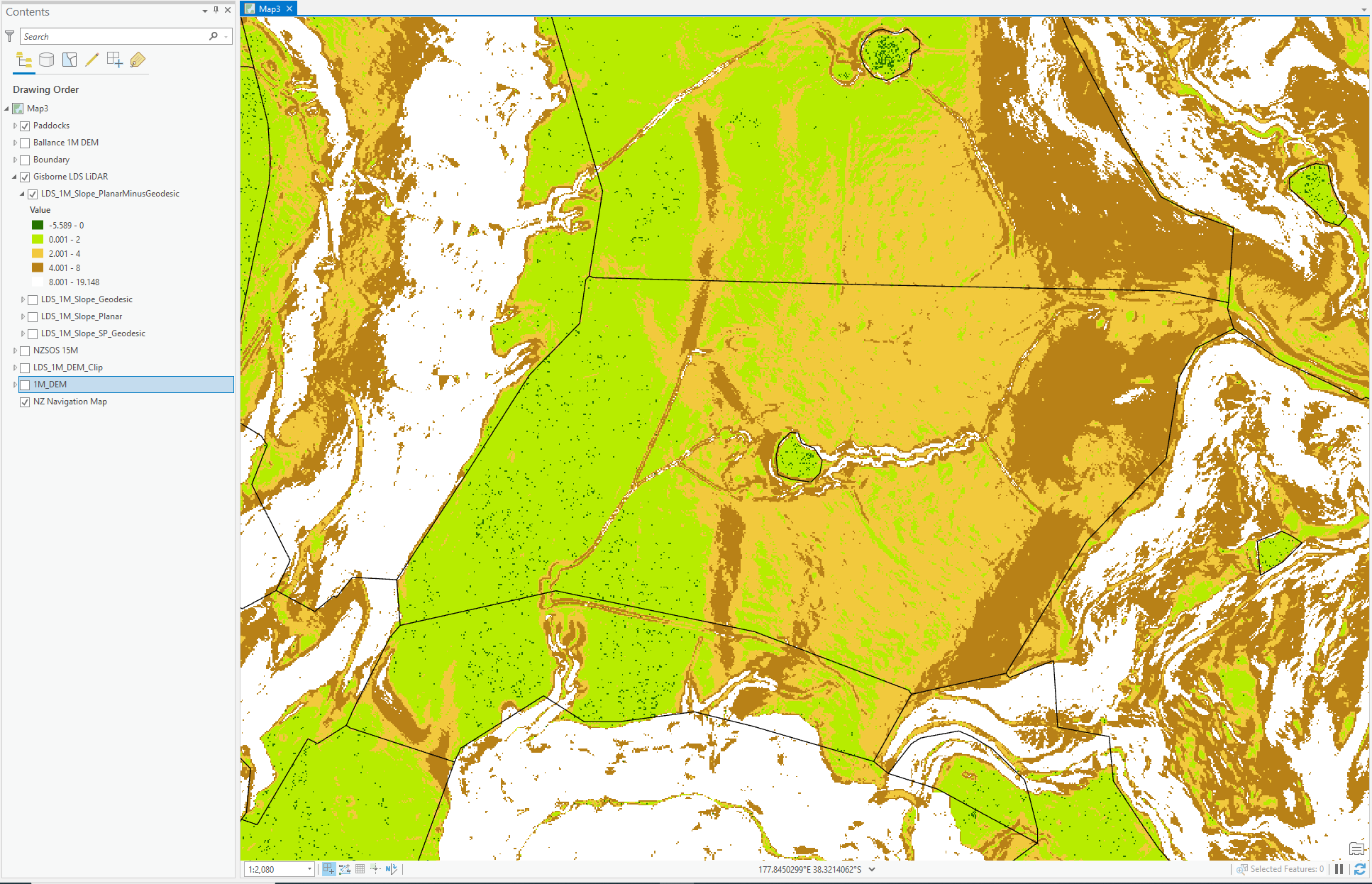
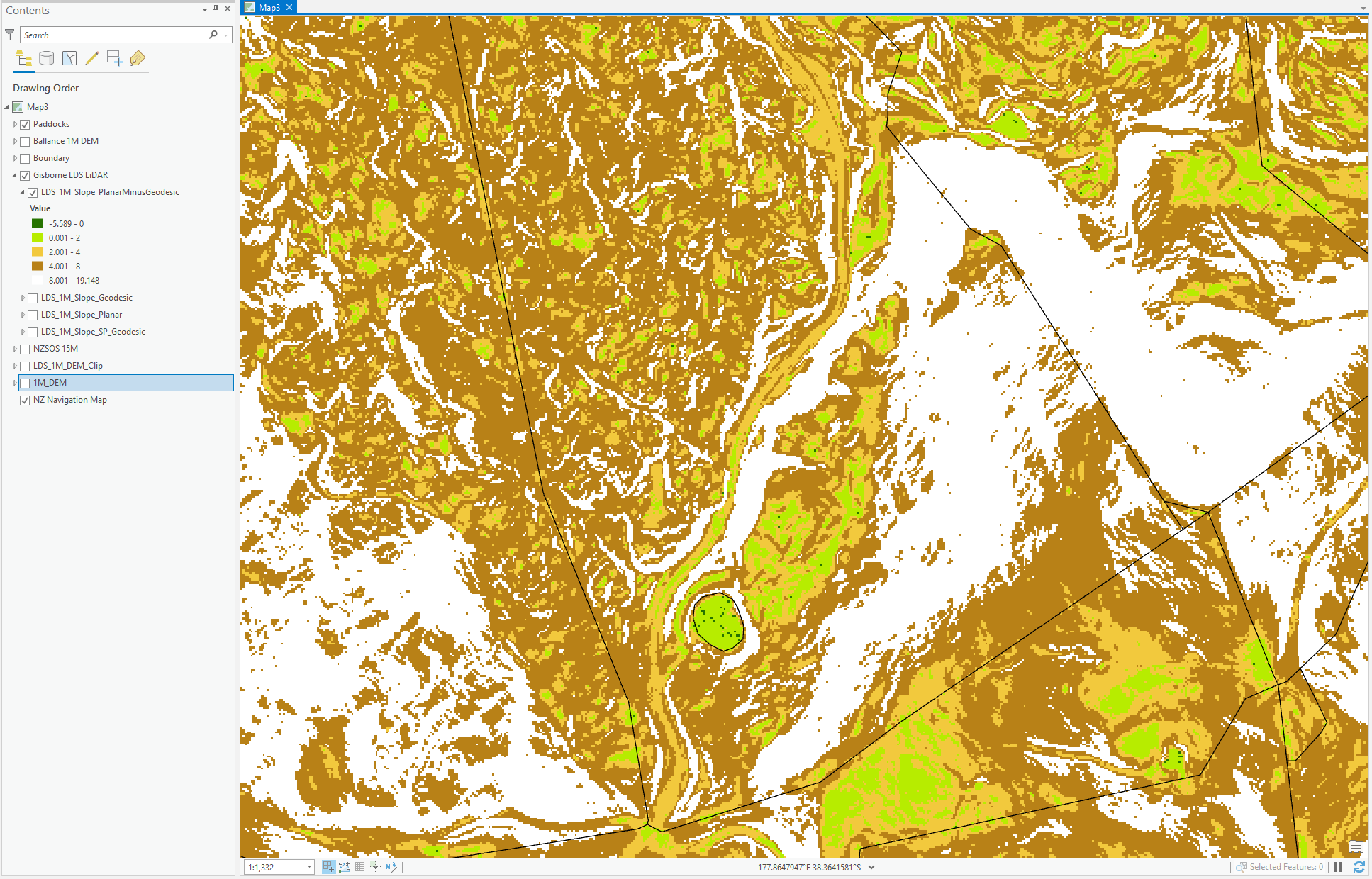
Geodesic_2GeodesicHere are the differences between the two, Green (<2 degrees difference) Brown (<8 degrees difference) White (>8 degrees)

DifferenceSurface_2DifferenceSurface

Geodesic should be the way to go. At least for 2022! 😀

The difference comes from the way distance is calculated between pixels (we will assume a raster DEM for this example). In planer the software uses the planar coordinate system on the data while in geodesic it transforms to a 3D spherical coordinate system and assumes some local normal planes.

In a planar coordinate system the distance between pixels is always the same value (a rectangular grid) while in a geodetic (3D) coordinate system the raster will be draped on a sphere (spheroid/ellipsoid) and the pixel distance will vary depending on the original projected coordinate system.

Depending on that (the coordinate system) and doing some statistics on your slope values, you should notice some constancy in slope percentage variation along some directions (ex: longitude/latitude/circles centered on the coordinate system pole).

So, comparing different calculated slopes by absolute values (what you did) is irrelevant. You should at least compare slope percentage change. This also will be mostly irrelevant but it should be easier to understand the phenomenon.

You can see from the your maps that the slope difference is bigger where the slope is bigger and smaller where the slope is smaller (or vice versa, you didn't show a legend of the ON layer for each map).

Do (planar_slope/geodesic_slope)-1 and get the rate of change from planar to geodesic and we will talk more on that.

Geodesic should be the way to go. At least for 2022! 😀

The difference comes from the way distance is calculated between pixels (we will assume a raster DEM for this example). In planer the software uses the planar coordinate system on the data while in geodesic it transforms to a 3D spherical coordinate system and assumes some local normal planes.

In a planar coordinate system the distance between pixels is always the same value (a rectangular grid) while in a geodetic (3D) coordinate system the raster will be draped on a sphere (spheroid/ellipsoid) and the pixel distance will vary depending on the original projected coordinate system.

Depending on that (the coordinate system) and doing some statistics on your slope values, you should notice some constancy in slope percentage variation along some directions (ex: longitude/latitude/circles centered on the coordinate system pole).

So, comparing different calculated slopes by absolute values (what you did) is irrelevant. You should at least compare slope percentage change. This also will be mostly irrelevant but it should be easier to understand the phenomenon.

You can see from the your maps that the slope difference is bigger where the slope is bigger and smaller where the slope is smaller (or vice versa, you didn't show a legend of the ON layer for each map).

Do (planar_slope/geodesic_slope)-1 and get the rate of change from planar to geodesic and we will talk more on that.

That's very good to know, thank you!! Its Friday night here so probably won't get back to you till after the weekend :)

Geodesic should be the way to go. At least for 2022! 😀

The difference comes from the way distance is calculated between pixels (we will assume a raster DEM for this example). In planer the software uses the planar coordinate system on the data while in geodesic it transforms to a 3D spherical coordinate system and assumes some local normal planes.

In a planar coordinate system the distance between pixels is always the same value (a rectangular grid) while in a geodetic (3D) coordinate system the raster will be draped on a sphere (spheroid/ellipsoid) and the pixel distance will vary depending on the original projected coordinate system.

Depending on that (the coordinate system) and doing some statistics on your slope values, you should notice some constancy in slope percentage variation along some directions (ex: longitude/latitude/circles centered on the coordinate system pole).

So, comparing different calculated slopes by absolute values (what you did) is irrelevant. You should at least compare slope percentage change. This also will be mostly irrelevant but it should be easier to understand the phenomenon.

You can see from the your maps that the slope difference is bigger where the slope is bigger and smaller where the slope is smaller (or vice versa, you didn't show a legend of the ON layer for each map).

Do (planar_slope/geodesic_slope)-1 and get the rate of change from planar to geodesic and we will talk more on that.

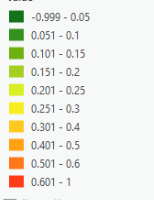
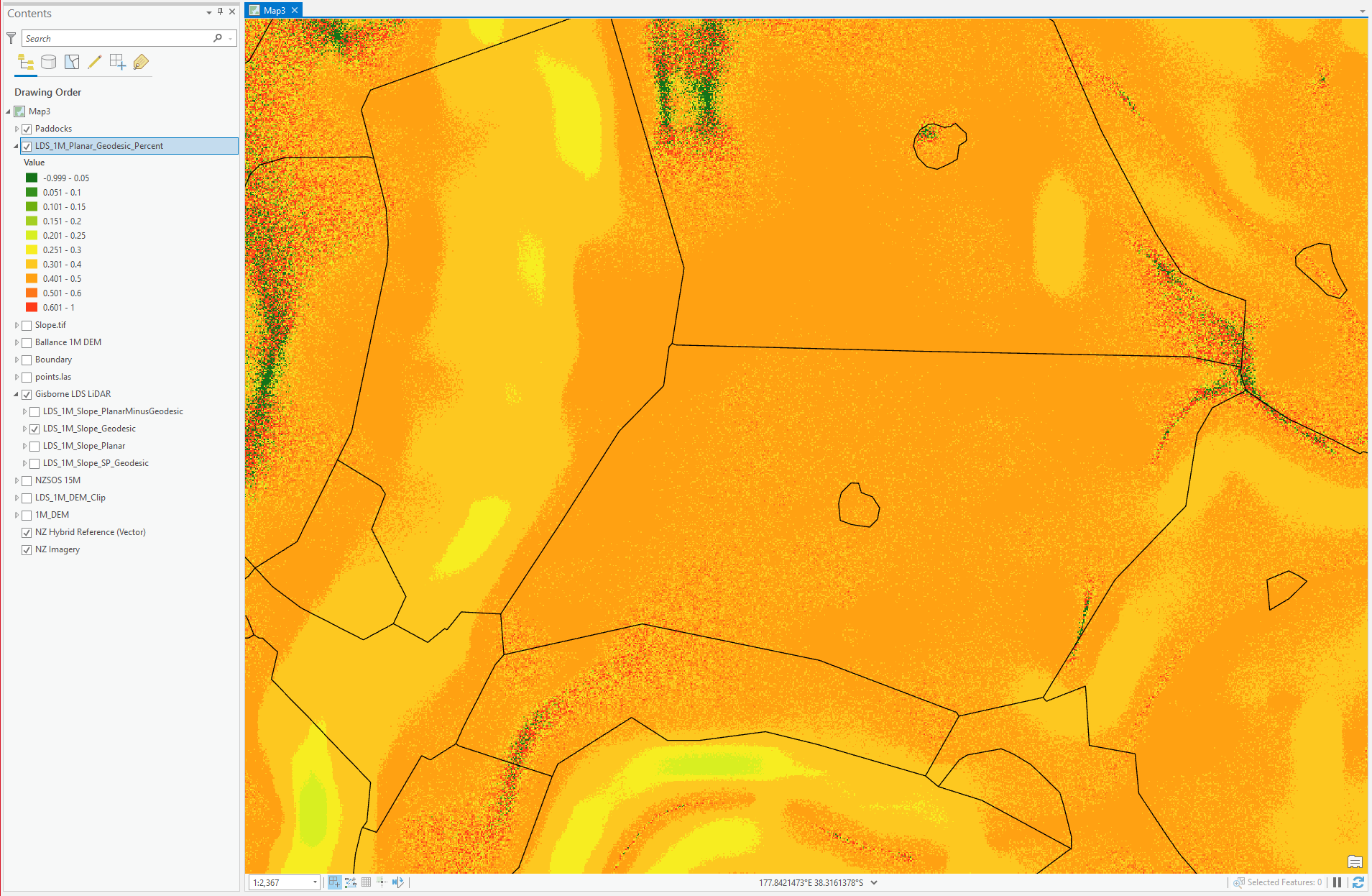
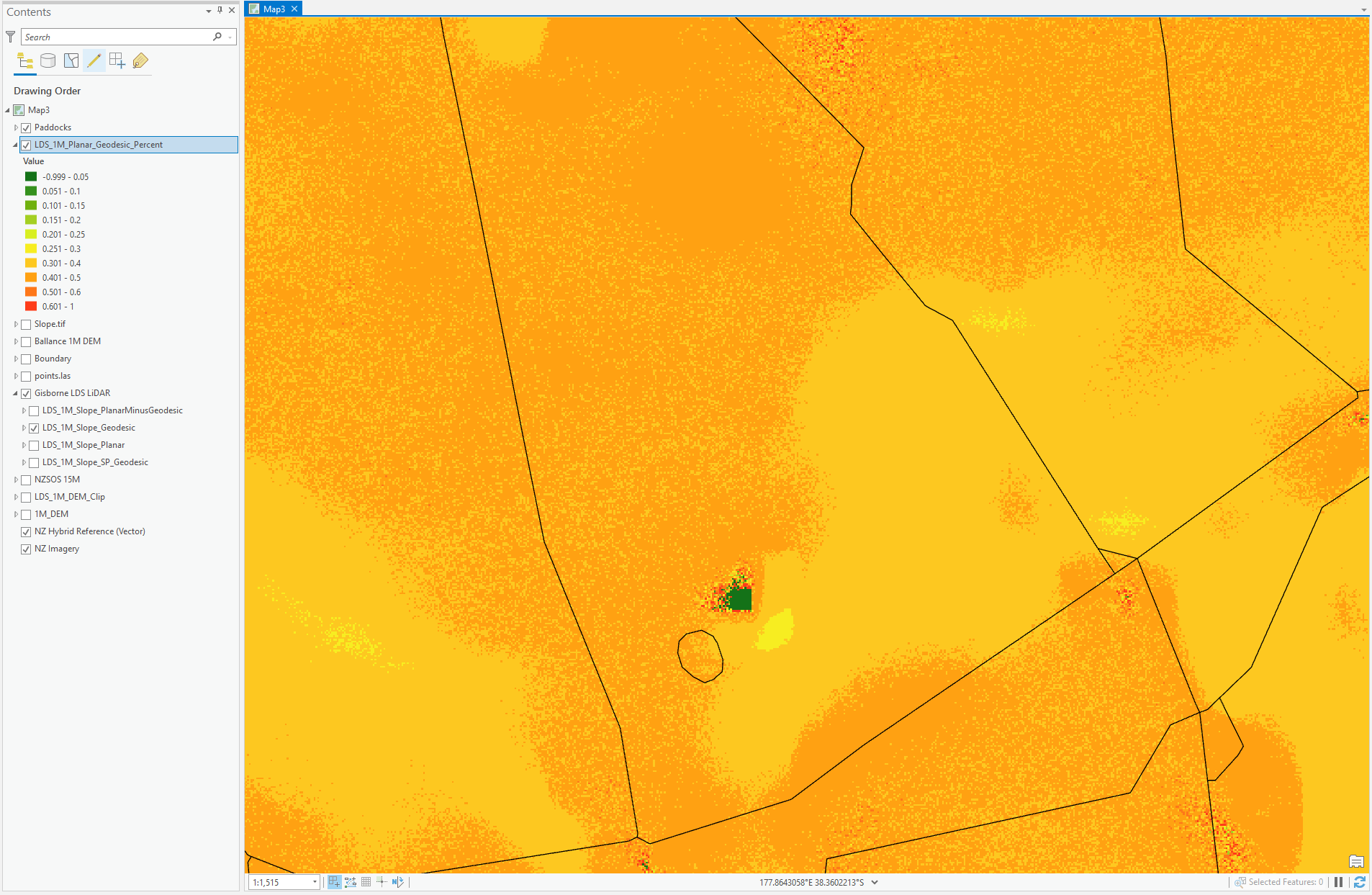Hi @caracadrian​ thanks for that response, heres the results of the rate of change calc:imageMicrosoftTeams-image (1)MicrosoftTeams-imageAs you can see, the difference between them all is ~40% across it all.

 

 

We get there should be a difference between the two, but are confused as to why the difference is so large

Hi @caracadrian​ thanks for that response, heres the results of the rate of change calc:imageMicrosoftTeams-image (1)MicrosoftTeams-imageAs you can see, the difference between them all is ~40% across it all.

 

 

We get there should be a difference between the two, but are confused as to why the difference is so large

This is very wrong.

I was expecting a variance of 1-2% across your area. Not 30%.

You either have the DEM in lat/long coordinates, some very, very weird projection or the algorithms are messed up. Either way, something is wrong. I never got such a difference from planar to geodesic in ArcMap, ArcGIS Pro or FME.

At this point some sample data would help. I can run it both in ArcGIS Pro and FME and get a better understanding. Also, please keep in mind that there is an 11 hours time difference between us.

Hi @caracadrian​ thanks for that response, heres the results of the rate of change calc:imageMicrosoftTeams-image (1)MicrosoftTeams-imageAs you can see, the difference between them all is ~40% across it all.

 

 

We get there should be a difference between the two, but are confused as to why the difference is so large

We were expecting similar differences (1-2%) as well. The DEM is in NZTM - meters for all measurements.

 

Here's a link to the file - https://abley-my.sharepoint.com/:i:/p/hamish/EUYq7py0lkFGrmSfnXLGSQgB8W5QBprOpZDWLm6f_ZfUUg?e=Ol1uZD

@hkingsbury​ I played with your data this morning.

I calculated the slope as percentage both in ArcGIS and FME and exported the slope rasters from ArcGIS to make a comparison.

In ArcGIS Pro I ran Slope from Analysis -> Tools -> Analyze Terrain -> Slope and set it as Percent rise, the same as in RasterSlopeCalculator in FME.

Screenshot 2022-03-29 104528Then, in FME I used RasterExpressionEvaluator set as Two Rasters and Expression Ab0]/B]0]-1, to make comparisons.

  • ArcGIS geodesic vs FME has around 25% rate of change for the Horn algorithm and 3.5% rate of change for Zevenberg and Thorne (FME algorithms, I didn't find an algorithm choice in ArcGIS).
  • ArcGIS planar vs FME has around 30% rate of change (constant).
  • ArcGIS planar vs ArcGIS geodesic has around 30% rate of change.

The x% isn't in the slope values, it's in the rate of change.

Except for a few pixels that are "out of bounds" everything looks constant.

I have attached the workspace where I did the comparison.

That being said, I think the algorithm maters, how the application interprets Nodata maters. ESRI isn't that open to document the algorithms used or what decision the application makes when choosing one over the other (if there are many).

I conclude that there is about the same difference between planar and geodesic no matter what software you use given you use the same algorithm.

@hkingsbury​ I played with your data this morning.

I calculated the slope as percentage both in ArcGIS and FME and exported the slope rasters from ArcGIS to make a comparison.

In ArcGIS Pro I ran Slope from Analysis -> Tools -> Analyze Terrain -> Slope and set it as Percent rise, the same as in RasterSlopeCalculator in FME.

Screenshot 2022-03-29 104528Then, in FME I used RasterExpressionEvaluator set as Two Rasters and Expression Ab0]/B]0]-1, to make comparisons.

  • ArcGIS geodesic vs FME has around 25% rate of change for the Horn algorithm and 3.5% rate of change for Zevenberg and Thorne (FME algorithms, I didn't find an algorithm choice in ArcGIS).
  • ArcGIS planar vs FME has around 30% rate of change (constant).
  • ArcGIS planar vs ArcGIS geodesic has around 30% rate of change.

The x% isn't in the slope values, it's in the rate of change.

Except for a few pixels that are "out of bounds" everything looks constant.

I have attached the workspace where I did the comparison.

That being said, I think the algorithm maters, how the application interprets Nodata maters. ESRI isn't that open to document the algorithms used or what decision the application makes when choosing one over the other (if there are many).

I conclude that there is about the same difference between planar and geodesic no matter what software you use given you use the same algorithm.

Thanks for looking into that. We're needing the degree of the slope, not the percentage change. Other than selecting degrees, that is the exact process we've been following

Reply


Community Stats

30,168
Posts
114,527
Replies
37,825
Members
Terms & ConditionsCookie settings
A product of
Safe Software respectfully acknowledges that we live, learn and work on the traditional and unceded territories of the Kwantlen, Katzie, and Semiahmoo First Nations.