Hi @aharport​ ,

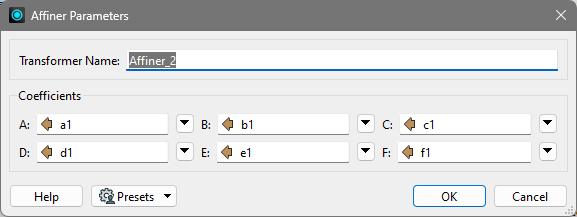
​I think you can calculate required coefficients for Affiner performing "inverse transformation" as elements of the inverse matrix of the original transformation matrix (A, B, C; D, E, F; 0, 0, 1).

However, the geometry restored with the inverse transformation may not be completely equal to the origional one, since you cannot avoid very small calculation error in such a math operation always.

If you intend to restore the original geometry in the local coordinate coordinate system after performing some processing in the RD83, I would recommend you to use GeometryExtractor (before the processing) and GeometryReplacer (after) rather than inverse transformation.

See the attached workspace example to learn more.

Hope this helps.

I don't know how to form the inverse matrix. Maybe you can help me with that?

If you download en open the attached workspace you can see how it is done in the AttributeManager.

Very nice. I completely agree with your comment regarding accuracy after the inverse transformation. If the coordinate precision is known for the original dataset (e.g. 6 significant digits), it might be possible to improve the result slightly by using a CoordinateRounder after the inverse transformation.

You can find some website which describe formula of inverse 3x3 matrix.

e.g.

https://ardoris.wordpress.com/2008/07/18/general-formula-for-the-inverse-of-a-3x3-matrix/

https://www.storyofmathematics.com/inverse-of-a-3x3-matrix/#3_x_3_Inverse_Matrix_Formula

The 3x3 matrix for affine transformation is a special case with g = h = 0 and i = 1, so you can simplify the formula. I applied the simplified formula in order to calculate coefficient for the inverse matrix in the AttributeManager.

Sorry, I can't open the workspace completely because I'm using an older FME version. Can someone save the workspace for the 2020 version again?

My lowest installed version is 2021 atm. You can install multiple versions next to each other on the same machine, just use different installation folders. FME downloads.

Here are the key formulas from @Takashi Iijima​'s workspace:

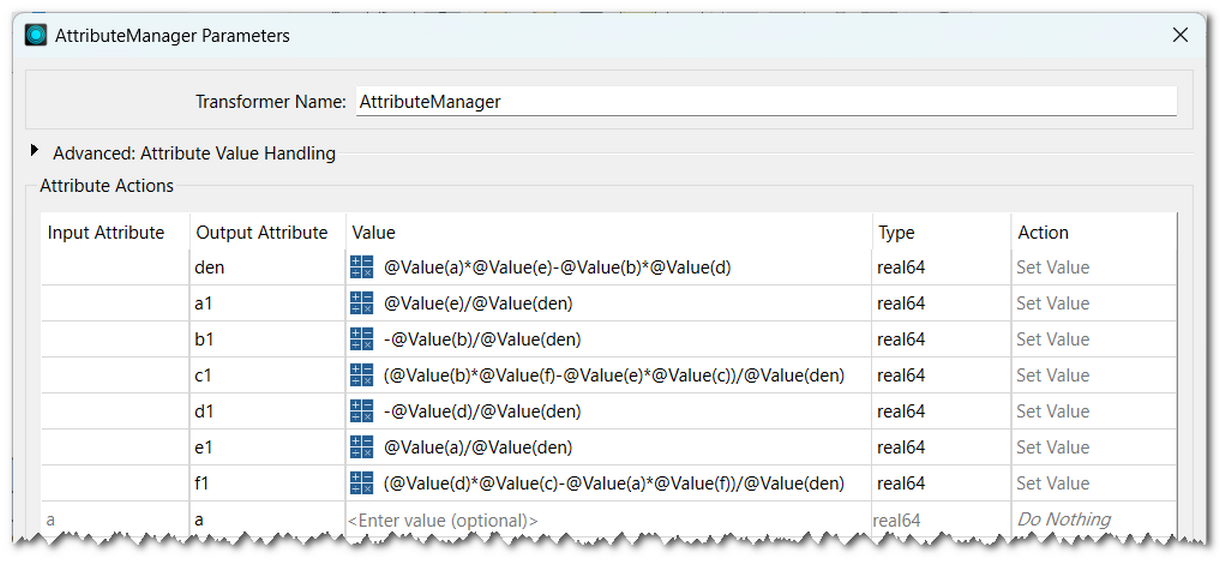
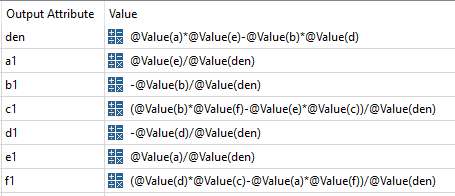The attributes a-f contain the values used in the first Affiner (the values posted in the question), the attributes a1-f1 will contain the values to use in the second Affiner to inverse the result of the first:

Unfortunately the AttributeManager in FME 2023.x is not compatible to previous versions of FME, so you cannot save the workspace example I posted for FME 2020. Instead, see this screenshot to see the math expressions to calculate coefficients of the inverse matrix (a1, b1, c1, ...) based on the coefficients of the original Affiner parameters (a, b, c, ...).

Thank you. I entered the math expressions (with @evaluate) into the AttributeManager. Unfortunately the run fails. All objects go into the rejected output.

Name of the @Value function should start with uppercase 'V'.

Use @Value(den) not @value(den).

Small mistake, big effect. Now it works! 😀

Thank you very much again for your support🙌