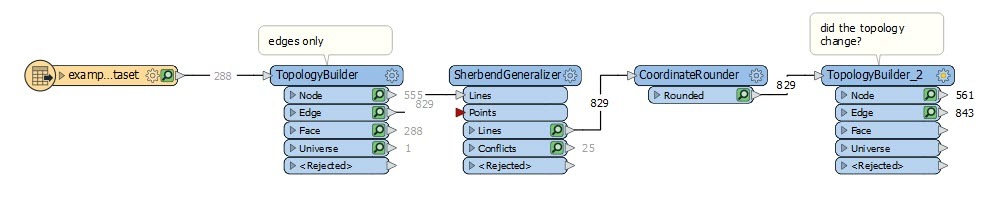
I have a polygon dataset, which amongst other things needs to have the coordinates of its vertices rounded to a centimeter. It seems that CoordinateRounder is not topology-aware, so I end up having self-intersections, which I cannot (completely) repair afterwards.
I'm new to FME, so maybe I am missing something here?





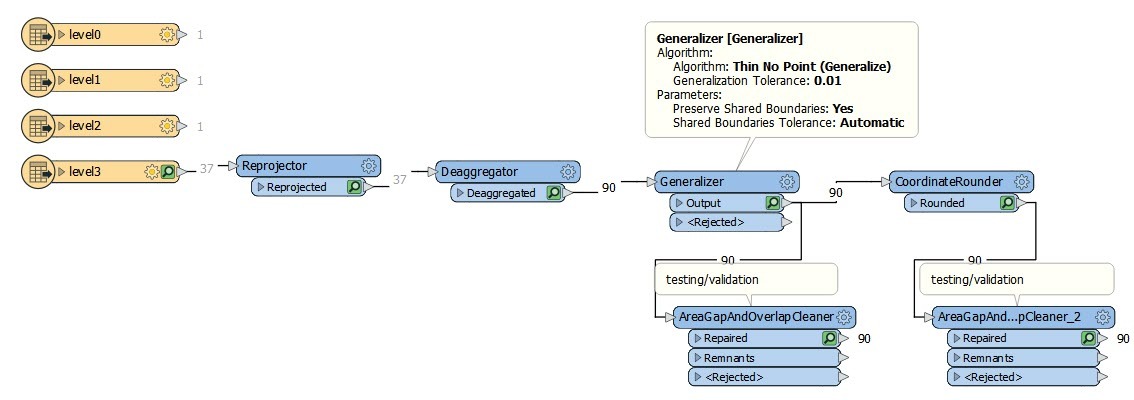 I've attached a small example using data from gadm36.org (FME 2020.2)
I've attached a small example using data from gadm36.org (FME 2020.2) generalized:
generalized: failed:
failed: passed:
passed: repaired:
repaired: ws:
ws: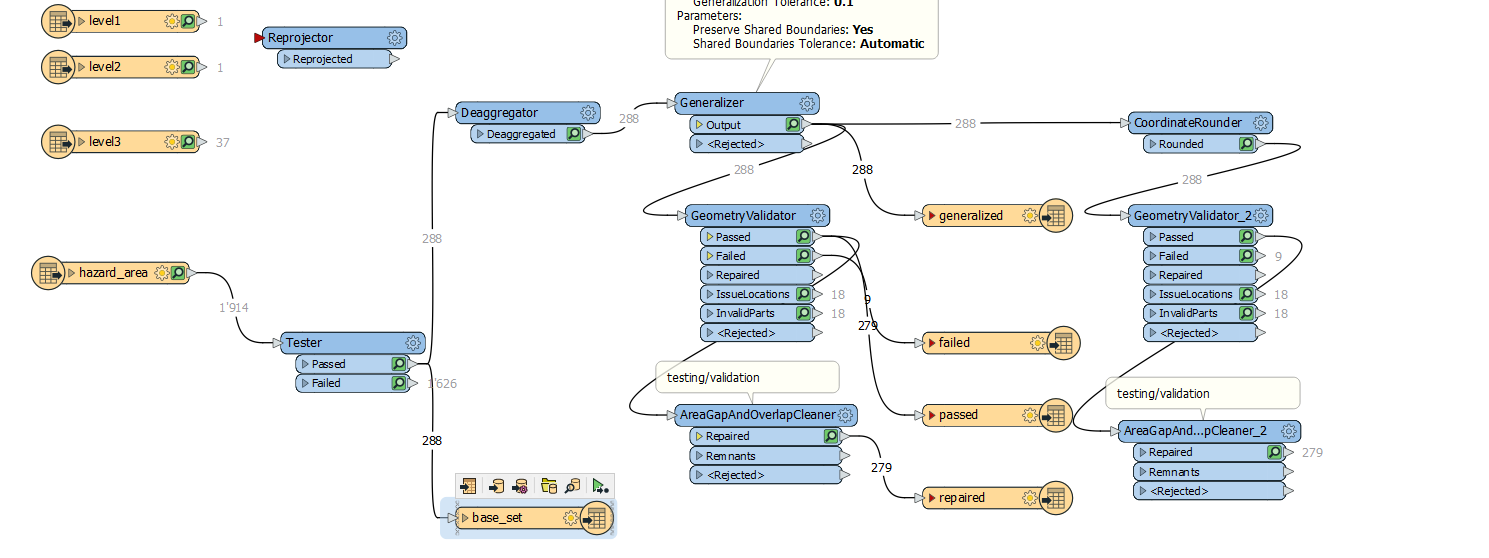




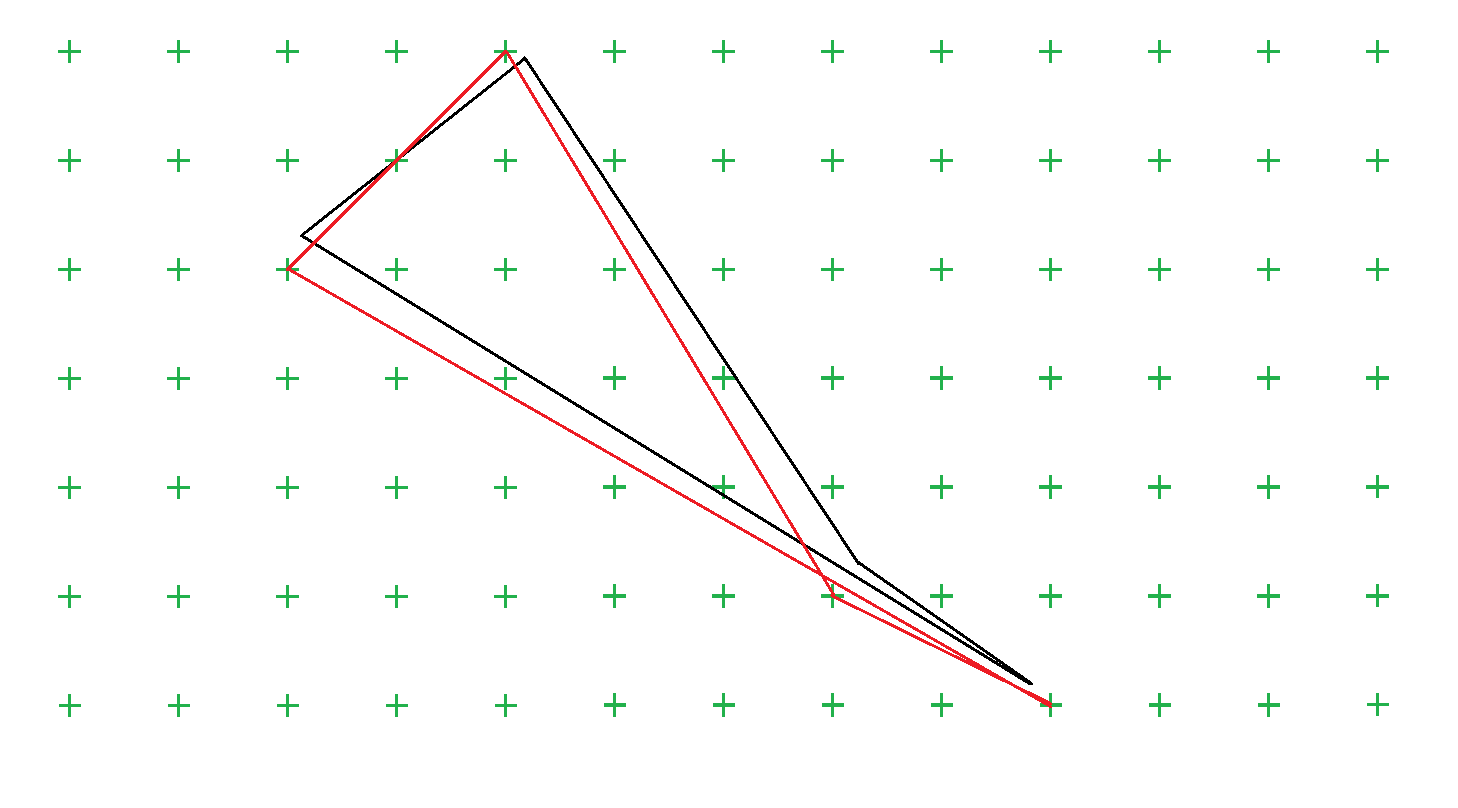 If all segments are longer than the Generalizer distance, nothing will happen to the geometry. The self-intersection after the rounding happens, because a (rounded) point jumps over a line.
If all segments are longer than the Generalizer distance, nothing will happen to the geometry. The self-intersection after the rounding happens, because a (rounded) point jumps over a line.