Skip to main content
  • EN

Hi all,

 

I am trying to find an FME solution to an optimisation problem.

 

I have ‘x’ polygons of varying sizes, the combined area of these polygons adds up to ‘y’. I need to allocate these polygons across ‘z’ number of groups, each of which require a different proportion of ‘y’.

 

For example:

·        10 polygons (x) of varying sizes with a combined total area of 62ha (y) that need to be proportionally allocated across three groups (z)

 

·        Group 1 – needs 60% of y (37.2 ha)

·        Group 2 – needs 30% of y (18.6 ha)

·        Group 3 – needs 10% of y (6.2 ha)

 

Possible solutions:

 

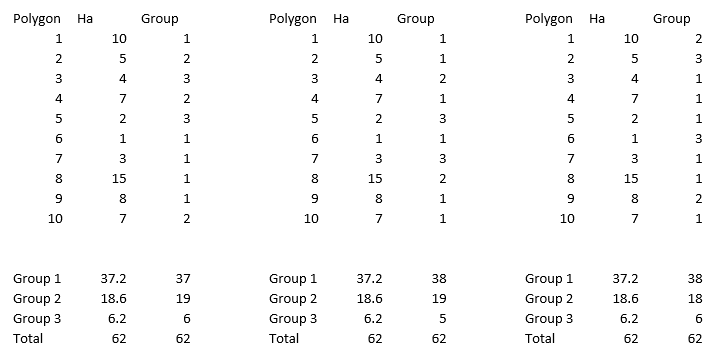example_solutionsI am after an optimised solution for the groupings of these polygons (in the above example, the first solution would be considered the closest to the allocation requirement).

 

Please note, I do not need to worry about the spatial position of these polygons, I just need to determine the best group allocation of each polygon so that I end up with the closest possible required outcome for each group.

 

Thanks!

 

Off-hand, I would split the data into smaller parts - like 1m squares - using the Tiler. Then I would sort all those parts using the SpatialSorter transformer. Then use a Sampler in the required proportions. So for 60-30-10 take the first 60% of the features, then the next 30%, then the final 10%, dissolving them back together.

 

That's my first thought anyway. I've had some success in the past using the SpatialSorter for things like this, you'd just have to break the polygons down first if you want a smaller resolution.

There's probably an algorithm out there which does this, if you can find the right search terms.

If I was to do this with python, first sort the numbers largest to smallest, then assign them to a group which would get its sum closest to the target sum for that group. That wouldn't get the optimal result though.

Maybe there's a way with the ShortestPathFinder, to find the smallest group of numbers within the set which add to the target? No obvious solution sorry.

Thanks for the replies.

 

@mark2atsafe​ unfortunately we can't have the polygons cut up. The polygons need to remain whole and just be allocated to achieve the best possible outcome (of course if there are some very large polygons and not many small polygons, this may result in a solution that is way off but that is ok as long as it is the 'best' solution).

 

@ctredinnick​ thanks for the suggestions, I have looked into this by using a Sorter and a StatisticsCalulator set to output cumulative results but as you say, it is not the optimal result, just a result. Finding the correct search terms for Google has been difficult!

 

I have also looked into the ListSubsetEnumerator which does look very promising. I have used this to create every possible combination of grouping and then determined which one was the closest to the desired outcome. The only issue being that it needs the number of elements in the group to be explicitly stated rather than trying every single possible combination (obviously this would be dangerous to allow considering the possible number of combination could be enormous). I may try to put the ListSubsetEnumerator into a custom looping transformer and have it cycle through different numbers of groupings before comparing all the answers to find the best one. This will quickly become very complex so I wanted to put something on the forum before trying it!

Ah, apologies, I thought that the spatial part was important. I guess it isn't. In that case, the term you are looking for is "the bin-packing problem" or (Wikipedia tells me) Combinatorial Optimization.

 

I don't think there's really a transformer in FME designed to handle that. But you might find that there are existing scripts in R or Python that you could run within FME. I suspect R is the more likely, since it's meant to be a statistical tool.

 

Good luck and let us know how you get on.

Ah, apologies, I thought that the spatial part was important. I guess it isn't. In that case, the term you are looking for is "the bin-packing problem" or (Wikipedia tells me) Combinatorial Optimization.

 

I don't think there's really a transformer in FME designed to handle that. But you might find that there are existing scripts in R or Python that you could run within FME. I suspect R is the more likely, since it's meant to be a statistical tool.

 

Good luck and let us know how you get on.

Oh, I should add that I had already added this as a request for a transformer. Its reference number is FMEEngine-52123. I also found that in spatial terms Esri calls this "Spatially Constrained Multivariate Clustering" - but of course, the spatial part isn't as important to you.

Off-hand, I would split the data into smaller parts - like 1m squares - using the Tiler. Then I would sort all those parts using the SpatialSorter transformer. Then use a Sampler in the required proportions. So for 60-30-10 take the first 60% of the features, then the next 30%, then the final 10%, dissolving them back together.

 

That's my first thought anyway. I've had some success in the past using the SpatialSorter for things like this, you'd just have to break the polygons down first if you want a smaller resolution.

Hi @mark2atsafe​ , after some further consideration of the problem, we decided that this methodology would produce a valid for our situation. Thank you for the idea, it will possibly come in handy elsewhere too!

Reply


Community Stats

30,171
Posts
114,533
Replies
37,830
Members
Terms & ConditionsCookie settings
A product of
Safe Software respectfully acknowledges that we live, learn and work on the traditional and unceded territories of the Kwantlen, Katzie, and Semiahmoo First Nations.