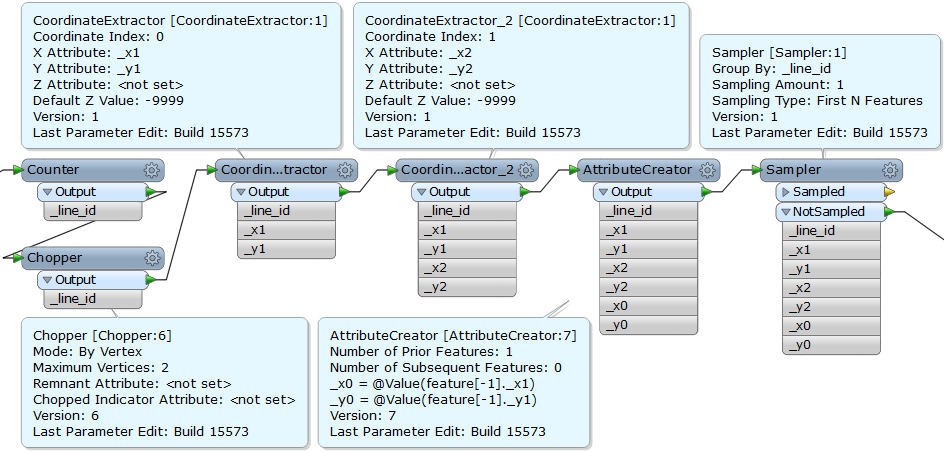
I have a line network and need to calculate the angle for each line vertex. I have tried using PolylineAnalyzer but unfortunately it doesn't calculate the angle for all vertices when I used it in the main workspace. Too many vertices miss the angle value.
As for now, I use PolylineAnalyzer in a second workspace which I execute for each line in the line network and write the results to a csv. This does, however, take a looong time. It is the attribute AngleBetweenLines I am after.