Hi,
I have finally outputted DTM into CityGML and thought I will share my experience and workspace with others. I also want to say thank you to Daen (FME support) for his help.
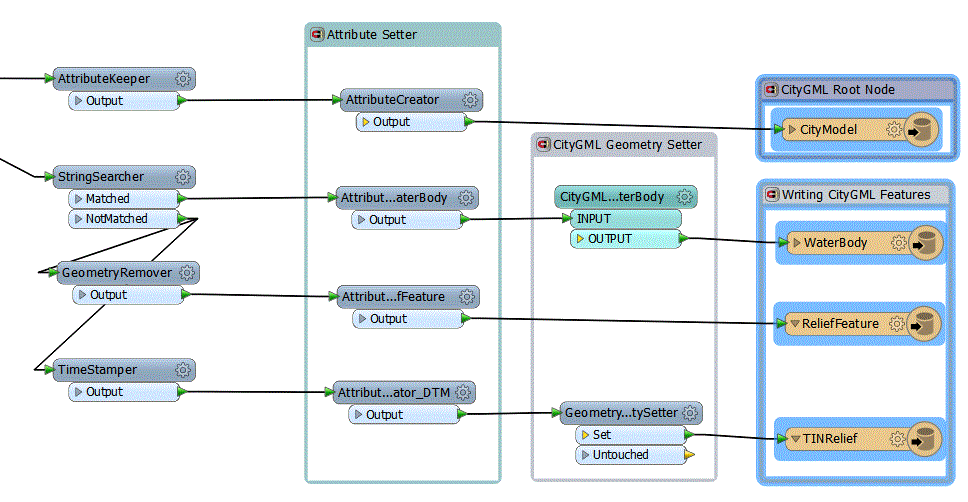
I had DTM defined as tin mesh and below is the workspace I created to convert it to ReliefFeature as TINRelief.
Two steps are needed:
First ReliefFeature has to be created (no geometry) to assign attribute gml_id="Example_ID"
Second TINRelief has to be created with:
gml_parent_id="Example_ID" (ReliefFeature parent)
citygml_feature_role=reliefComponent
citygml_lod_name=tin
citygml_level_of_detail=0 (or anything between 0-4)
Hope it helps.
barani
PS. I have also found this relevent text in the CityGML Implementation Specyfication (OGC 07-062) for reference:
" An essential part of a city model is the terrain. In CityGML, the terrain is represented by the class ReliefFeature in LOD 0-4 (Fig. 21 depicts the UML diagram, for XML schema definition see chapter 10.4.8). A ReliefFeature consists of one or more entities of the class ReliefComponent. Its validity may be restricted to a certain area defined by an optional validity extent polygon. As ReliefFeature and ReliefComponent are derivatives of CityOb-ject, the corresponding attributes and relations are inherited. The class ReliefFeature is associated with different concepts of terrain representations which can coexist. The terrain may be specified as a regular raster or grid (RasterRelief), as a TIN (Triangulated Irregular Network, TINReflief), by break lines (BreaklineRelief), or by mass points (MasspointRelief). The four types are implemented by the corresponding GML3 classes: grids by RectifiedGridCoverages, break lines by Curves, mass points by Points and TINs either by TriangulatedSurfaces or by GML3 TINs. In case of TriangulatedSurfaces, the triangles are given explicitly while in case of GML3 TINs only 3D points are represented, where the triangulation can be reconstructed by standard methods (Delau-nay triangulation, cf. Okabe et al. 1992). Break lines are represented by 3D curves. Mass points are simply a set of 3D points."

