Skip to main content
  • EN

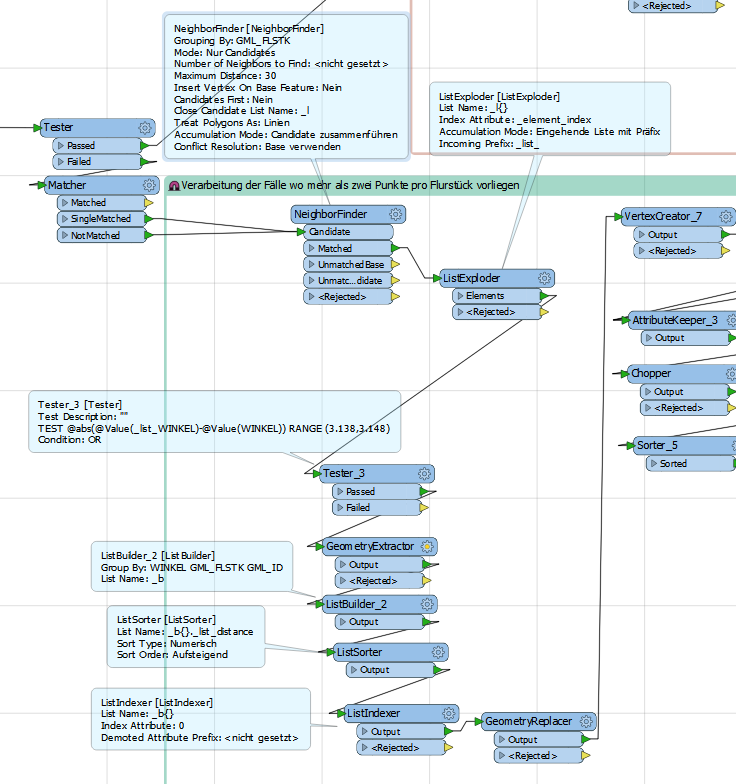
Hello,

I need to find those two pair of points that correspond to the following rule:

1. Corresponding points share the same MAIN_ID

2. The absolute value of the difference of attribute value WINKEL of the two corresponding points is exactly 3.14 (pi)

3. The points are within a certain distance to each other

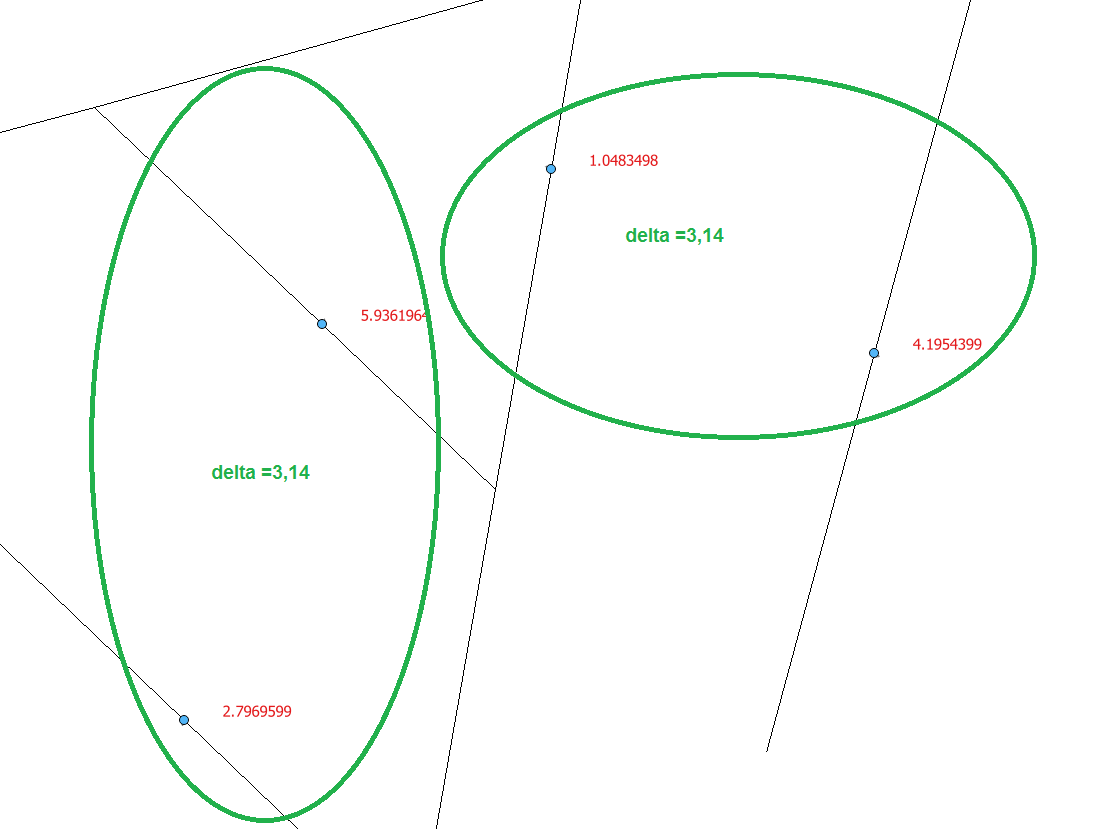
In the following Image you see 4 points that share the same MAIN_ID. However, it could be many more points. All points have an attrribute WINKEL, the values are labelled in red. The green ellipses mark the pair of points that belong together.

Any clue how to achieve this without using python?

You can cover #1 and #3 with a NeighborFinder, grouping by MAIN_ID, and I think I've got the rest worked out like this:

The test is @abs(@Value(_list_number)-@Value(number)) = 8

 

(in your case that would be 3,14)

I don't think I'm all the way there yet, but this should hopefully give you some pointers.

none2none.fmw

 

This may work, but there is some question over rounding precision when using Pi (e.g.in the examples the delta doesn't exactly correspond to 3.14) and it assumes that there will only ever be one match

With the output looking like this

looks like points on reversed lines with a certain distance and sharing an ID. (parallel but reversed.)

That would mean, if it were exactly pi differing, that all points on the line have the same distance to the corresponding match.

So why not test for that.

Hi @redgeographics, @gio and @egomm,

thank you very much for your support! Your hints inspired me and I am now there where I wanted to be. Since there are also situations where more than two Points

meet the above stated conditions I had to also add a sorting by distance and picking the smallest value (nearest distance).

Attached you find a screenshot of the snippet that does the job:

Reply


Community Stats

30,126
Posts
114,372
Replies
37,765
Members
Terms & ConditionsCookie settings
A product of
Safe Software respectfully acknowledges that we live, learn and work on the traditional and unceded territories of the Kwantlen, Katzie, and Semiahmoo First Nations.